
已知二次函數y=f1(x)的圖象以原點為頂點且過點(1,1),反比例函數y=f2(x)的圖象與直線y=x的兩個交點間距離為8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函數f(x)的表達式;
(Ⅱ) 證明:當a>3時,關于x的方程f(x)= f(a)有三個實數解.
(Ⅰ) f(x)=x2+ .(Ⅱ) f(x)=f(a),得x2+
.(Ⅱ) f(x)=f(a),得x2+ =a2+
=a2+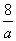 , 即
, 即 =-x2+a2+
=-x2+a2+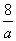 .在同一坐標系內作出f2(x)=
.在同一坐標系內作出f2(x)= 和f3(x)= -x2+a2+
和f3(x)= -x2+a2+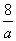 的大致圖象,其中f2(x)的圖象是以坐
的大致圖象,其中f2(x)的圖象是以坐
標軸為漸近線,且位于第一、三象限的雙曲線, f3(x)與的圖象是以(0, a2+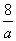 )為頂點,開口向下的拋物線.因此, f2(x)與f3(x)的圖象在第三象限有一個交點,即f(x)=f(a)有一個負數解.又∵f2(2)="4," f3(2)= -4+a2+
)為頂點,開口向下的拋物線.因此, f2(x)與f3(x)的圖象在第三象限有一個交點,即f(x)=f(a)有一個負數解.又∵f2(2)="4," f3(2)= -4+a2+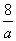 ,當a>3時,. f3(2)-f2(2)= a2+
,當a>3時,. f3(2)-f2(2)= a2+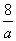 -8>0,當a>3時,在第一象限f3(x)的圖象上存在一點(2,f(2))在f2(x)圖象的上方.f2(x)與f3(x)的圖象在第一象限有兩個交點,即f(x)=f(a)有兩個正數解.因此,方程f(x)=f(a)有三個實數解.
-8>0,當a>3時,在第一象限f3(x)的圖象上存在一點(2,f(2))在f2(x)圖象的上方.f2(x)與f3(x)的圖象在第一象限有兩個交點,即f(x)=f(a)有兩個正數解.因此,方程f(x)=f(a)有三個實數解.
解析試題分析:(Ⅰ)由已知,設f1(x)=ax2,由f1(1)=1,得a="1," ∴f1(x)= x2.設f2(x)= (k>0),它的圖象與直線y=x的交點分別為A(
(k>0),它的圖象與直線y=x的交點分別為A(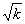 ,
,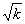 ),B(-
),B(-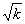 ,-
,-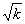 )
)
由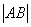 =8,得k="8,." ∴f2(x)=
=8,得k="8,." ∴f2(x)= .故f(x)=x2+
.故f(x)=x2+ .
.
(Ⅱ) (證法一)f(x)=f(a),得x2+ =a2+
=a2+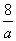 ,
,
即 =-x2+a2+
=-x2+a2+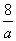 .在同一坐標系內作出f2(x)=
.在同一坐標系內作出f2(x)= 和
和
f3(x)= -x2+a2+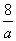 的大致圖象,其中f2(x)的圖象是以坐
的大致圖象,其中f2(x)的圖象是以坐
標軸為漸近線,且位于第一、三象限的雙曲線, f3(x)與的圖象是以(0, a2+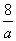 )為頂點,開口向下的拋物線.因此, f2(x)與f3(x)的圖象在第三象限有一個交點,即f(x)=f(a)有一個負數解.又∵f2(2)="4," f3(2)= -4+a2+
)為頂點,開口向下的拋物線.因此, f2(x)與f3(x)的圖象在第三象限有一個交點,即f(x)=f(a)有一個負數解.又∵f2(2)="4," f3(2)= -4+a2+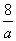 ,當a>3時,. f3(2)-f2(2)= a2+
,當a>3時,. f3(2)-f2(2)= a2+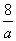 -8>0,當a>3時,在第一象限f3(x)的圖象上存在一點(2,f(2))在f2(x)圖象的上方.f2(x)與f3(x)的圖象在第一象限有兩個交點,即f(x)=f(a)有兩個正數解.因此,方程f(x)=f(a)有三個實數解.
-8>0,當a>3時,在第一象限f3(x)的圖象上存在一點(2,f(2))在f2(x)圖象的上方.f2(x)與f3(x)的圖象在第一象限有兩個交點,即f(x)=f(a)有兩個正數解.因此,方程f(x)=f(a)有三個實數解.
(證法二)由f(x)=f(a),得x2+ =a2+
=a2+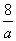 ,即(x-a)(x+a-
,即(x-a)(x+a-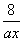 )=0,得方程的一個解x1=a.方程x+a-
)=0,得方程的一個解x1=a.方程x+a-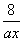 =0化為ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2=
=0化為ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2= , x3=
, x3=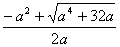 ,x2<0, x3>0, ∵x1≠ x2,且x2≠ x3.若x1= x3,即a=
,x2<0, x3>0, ∵x1≠ x2,且x2≠ x3.若x1= x3,即a=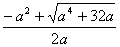 ,則3a2=
,則3a2= , a4=4a,得a=0或a=
, a4=4a,得a=0或a=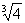 ,這與a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三個實數解.
,這與a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三個實數解.
考點:本題考查了函數與方程的運用
點評:函數與方程是高中數學重要的數學思想, 將函數問題轉化為方程問題求解,可以使函數中好多問題變得比較好解決


科目:高中數學 來源: 題型:解答題
(本題滿分13分)設函數
 滿足:
滿足: 都有
都有 ,且
,且 時,
時, 取極小值
取極小值
(1) 的解析式;
的解析式;
(2)當 時,證明:函數圖象上任意兩點處的切線不可能互相垂直;
時,證明:函數圖象上任意兩點處的切線不可能互相垂直;
(3)設 , 當
, 當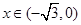 時,求函數
時,求函數 的最小值,并指出當
的最小值,并指出當 取最小值時相應的
取最小值時相應的 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
(本小題滿分12分)某地方政府準備在一塊面積足夠大的荒地上建一如圖所示的一個矩形綜合性休閑廣場,其總面積為3000平方米,其中場地四周(陰影部分)為通道,通道寬度均為2米,中間的三個矩形區域將鋪設塑膠地面作為運動場地(其中兩個小場地形狀相同),塑膠運動場地占地面積為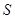 平方米.
平方米.
(1)分別寫出用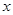 表示
表示 和用
和用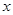 表示
表示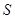 的函數關系式(寫出函數定義域);
的函數關系式(寫出函數定義域);
(2)怎樣設計能使S取得最大值,最大值為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com