
| A. | ($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2) | B. | ($\frac{1}{2}$,2) | C. | (-$\frac{1}{2}$,-2) | D. | ($\frac{1}{2}$,-2) |
分析 求出y′=-$\frac{1}{{x}^{2}}$,設(shè)P(x0,$\frac{1}{{x}_{0}}$),由在點(diǎn)P處的切線斜率為-4,利用導(dǎo)數(shù)的幾何意義得到-$\frac{1}{{{x}_{0}}^{2}}$=-4,由此能求出點(diǎn)P的坐標(biāo).
解答 解:∵曲線y=$\frac{1}{x}$,∴y′=-$\frac{1}{{x}^{2}}$,
設(shè)P(x0,$\frac{1}{{x}_{0}}$),
∵在點(diǎn)P處的切線斜率為-4,∴-$\frac{1}{{{x}_{0}}^{2}}$=-4,解得${x}_{0}=\frac{1}{2}$或${x}_{0}=-\frac{1}{2}$,
∴點(diǎn)P的坐標(biāo)是($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2).
故選:A.
點(diǎn)評 本題考查點(diǎn)的坐標(biāo)的求法,涉及到導(dǎo)數(shù)、切線、導(dǎo)數(shù)的幾何意義關(guān)系等基礎(chǔ)知識,考查推理論證能力、運(yùn)算求解能力、空間想象能力,考查化歸與轉(zhuǎn)化思想,是中檔題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
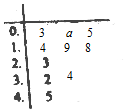 已知函數(shù)f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,現(xiàn)有一組數(shù)據(jù)(該組數(shù)據(jù)數(shù)量龐大),從中隨機(jī)抽取10個,繪制所得的莖葉圖如圖所示,且莖葉圖中的數(shù)據(jù)的平均數(shù)為2.
已知函數(shù)f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,現(xiàn)有一組數(shù)據(jù)(該組數(shù)據(jù)數(shù)量龐大),從中隨機(jī)抽取10個,繪制所得的莖葉圖如圖所示,且莖葉圖中的數(shù)據(jù)的平均數(shù)為2.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5人 | B. | 6人 | C. | 7人 | D. | 8人 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com