
已知函數 .
.
(1)若a=2,求曲線y=f(x)在x=1處的切線方程;
(2)求f(x)的單調區間;
(3)設 ,若對任意
,若對任意 ,均存在
,均存在 ,使得
,使得 ,求a的取值范圍.
,求a的取值范圍.
(1) ;
;
(2)函數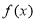 的單調遞增區間為
的單調遞增區間為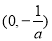 ,單調遞減區間為
,單調遞減區間為 ;
;
(3)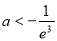 .
.
【解析】
試題分析:(1)把a的值代入f(x)中,求出f(x)的導函數,把x=1代入導函數中求出的導函數值即為切線的斜率,可得曲線y=f(x)在x=1處的切線方程;(2)求出f(x)的導函數,分a大于等于0和a小于0兩種情況討論導函數的正負,進而得到函數的單調區間;(3)對任意 ,均存在
,均存在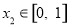 ,使得
,使得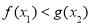 ,等價于
,等價于 ,分別求出相應的最大值,即可求得實數a的取值范圍.
,分別求出相應的最大值,即可求得實數a的取值范圍.
試題解析:【解析】
(1)由已知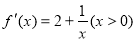 ,
, 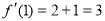 ,所以斜率
,所以斜率 ,
,
又切點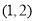 ,所以切線方程為
,所以切線方程為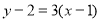 ),即
),即
故曲線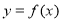 在
在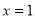 處切線的切線方程為
處切線的切線方程為 。
。
(2)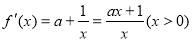
①當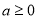 時,由于
時,由于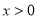 ,故
,故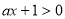 ,
,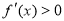 ,所以
,所以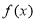 的單調遞增區間為
的單調遞增區間為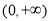 .
.
②當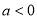 時,由
時,由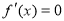 ,得
,得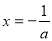 .
.
在區間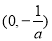 上,
上,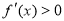 ,在區間
,在區間 上,
上,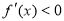 ,
,
所以,函數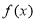 的單調遞增區間為
的單調遞增區間為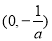 ,單調遞減區間為
,單調遞減區間為 .
.
(3)由已知,轉化為 .
.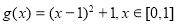 ,所以
,所以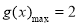
由(2)知,當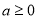 時,
時,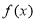 在
在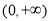 上單調遞增,值域為
上單調遞增,值域為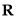 ,故不符合題意.
,故不符合題意.
(或者舉出反例:存在 ,故不符合題意.)
,故不符合題意.)
當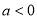 時,
時,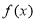 在
在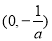 上單調遞增,在
上單調遞增,在 上單調遞減,
上單調遞減,
故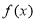 的極大值即為最大值,
的極大值即為最大值, ,
,
所以 , 解得
, 解得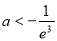 .
.
考點:1.利用導數研究曲線上某點切線方程;2.利用導數研究函數的單調性;3.利用導數求閉區間上函數的最值.


科目:高中數學 來源:2015屆四川省高三10月月考理科數學試卷(解析版) 題型:選擇題
如圖所示的莖葉圖表示甲、乙兩人在5次綜合測評中的成績,其中一個數字被污損,則甲的平均成績超過乙的平均成績的概率為( )

A. B.
B.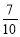 C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2015屆四川省巴蜀好教育聯盟12月大聯考理科數學試卷(解析版) 題型:選擇題
已知函數f(x)=sin(2x+Φ),其中Φ∈(0,2π),若f(x)≤|f(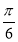 )|對一切x∈R恒成立,且f(
)|對一切x∈R恒成立,且f(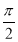 )<f(π),則f(x)的單調遞增區間是( )
)<f(π),則f(x)的單調遞增區間是( )
A、[kπ+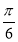 ,kπ+
,kπ+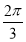 ](k∈Z)
](k∈Z)
B、[kπ-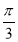 ,kπ+
,kπ+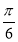 ](k∈Z)
](k∈Z)
C、[kπ,kπ+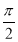 ](k∈Z)
](k∈Z)
D、[kπ-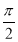 ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中數學 來源:2015屆四川省巴蜀好教育聯盟12月大聯考文科數學試卷(解析版) 題型:填空題
設f(x)= ,且f(8)=2,則f(f(80))=________________.
,且f(8)=2,則f(f(80))=________________.
查看答案和解析>>
科目:高中數學 來源:2015屆四川省巴蜀好教育聯盟12月大聯考文科數學試卷(解析版) 題型:選擇題
下列命題中的假命題是( )
A、?x∈R,lgx=0
B、?x∈R,tanx=2
C、?x∈R,2x>0
D、?x∈R,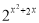 >1
>1
查看答案和解析>>
科目:高中數學 來源:2015屆吉林省吉林市高三第一次摸底考試理科數學試卷(解析版) 題型:解答題
已知 中, a,b, c 為角 A,B,C 所對的邊,
中, a,b, c 為角 A,B,C 所對的邊,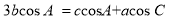 .
.
(1)求 cos A的值;
(2)若 的面積為
的面積為 ,求 b , c 的長.
,求 b , c 的長.
查看答案和解析>>
科目:高中數學 來源:2015屆吉林省吉林市高三第一次摸底考試理科數學試卷(解析版) 題型:選擇題
已知雙曲線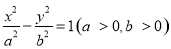 的左頂點與拋物線
的左頂點與拋物線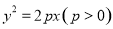 的焦點的距離為 4,的焦距是且雙曲線的一條漸近線與拋物線的準線的交點坐標為 (-2,- 1),則雙曲線的焦距為( )
的焦點的距離為 4,的焦距是且雙曲線的一條漸近線與拋物線的準線的交點坐標為 (-2,- 1),則雙曲線的焦距為( )
A. B.
B.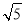 C.
C.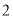 D.
D.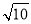
查看答案和解析>>
科目:高中數學 來源:2015屆北京市朝陽區高三上學期期中統一考試理科數學試卷(解析版) 題型:填空題
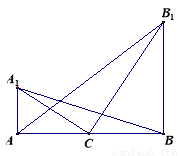
如圖,在水平地面上有兩座直立的相距60 m的鐵塔 和
和 .已知從塔
.已知從塔 的底部看塔
的底部看塔 頂部的仰角是從塔
頂部的仰角是從塔 的底部看塔
的底部看塔 頂部的仰角的2倍,從兩塔底部連線中點
頂部的仰角的2倍,從兩塔底部連線中點 分別看兩塔頂部的仰角互為余角.則從塔
分別看兩塔頂部的仰角互為余角.則從塔 的底部看塔
的底部看塔 頂部的仰角的正切值為 ;塔
頂部的仰角的正切值為 ;塔 的高為 m.
的高為 m.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com