
【題目】已知拋物線E:![]() 焦點F,過點F且斜率為2的直線與拋物線交于A、B兩點,且
焦點F,過點F且斜率為2的直線與拋物線交于A、B兩點,且![]() .
.
(1)求拋物線E的方程;
(2)設O是坐標原點,P,Q是拋物線E上分別位于x軸兩側的兩個動點,且![]()
①證明:直線PQ必過定點,并求出定點G的坐標;
②過G作PQ的垂線交拋物線于C,D兩點,求四邊形PCQD面積的最小值.
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2﹣2x﹣4y+m=0.
(1)若圓C與直線l:x+2y﹣4=0相交于M、N兩點,且|MN|![]() ,求m的值;
,求m的值;
(2)在(1)成立的條件下,過點P(2,1)引圓的切線,求切線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地因受天氣,春季禁漁等因素影響,政府規定每年的7月1日以后的100天為當年的捕魚期.某漁業捕撈隊對噸位為![]() 的20艘捕魚船一天的捕魚量進行了統計,如下表所示:
的20艘捕魚船一天的捕魚量進行了統計,如下表所示:
捕魚量(單位:噸) |
|
|
|
|
|
頻數 | 2 | 7 | 7 | 3 | 1 |
根據氣象局統計近20年此地每年100天的捕魚期內的晴好天氣情況如下表(捕魚期內的每個晴好天氣漁船方可捕魚,非晴好天氣不捕魚):
晴好天氣(單位:天) |
|
|
|
|
|
頻數 | 2 | 7 | 6 | 3 | 2 |
(同組數據以這組數據的中間值作代表)
(Ⅰ)估計漁業捕撈隊噸位為![]() 的漁船一天的捕魚量的平均數;
的漁船一天的捕魚量的平均數;
(Ⅱ)若以(Ⅰ)中確定的平均數作為上述噸位的捕魚船在晴好天氣捕魚時一天的捕魚量.
①估計一艘上述噸位的捕魚船一年在捕魚期內的捕魚總量;
②已知當地魚價為2萬元/噸,此種捕魚船在捕魚期內捕魚時,每天成本為10萬元/艘;若不捕魚,每天成本為2萬元/艘,請依據往年天氣統計數據,估計一艘此種捕魚船年利潤不少于1600萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的漸近線方程為
的漸近線方程為![]() ,一個焦點為
,一個焦點為![]() .
.
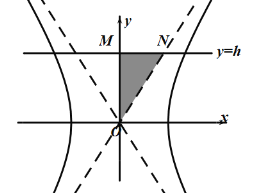
(1)求雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 上的任意一點
上的任意一點![]() ,分別作這兩條漸近線的平行線與這兩條漸近線得到四邊形
,分別作這兩條漸近線的平行線與這兩條漸近線得到四邊形![]() ,證明四邊形
,證明四邊形![]() 的面積是一個定值;
的面積是一個定值;
(3)設直線![]() 與
與![]()
![]() 在第一象限內與漸近線
在第一象限內與漸近線![]() 所圍成的三角形
所圍成的三角形![]() 繞著
繞著![]() 軸旋轉一周所得幾何體的體積.
軸旋轉一周所得幾何體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 為橢圓的左、右焦點,過右焦點
為橢圓的左、右焦點,過右焦點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若點A是第一象限內橢圓上一點,且在![]() 軸上的正投影為右焦點
軸上的正投影為右焦點![]() ,過點
,過點![]() 作直線
作直線![]() 分別交橢圓于
分別交橢圓于![]() 兩點,當直線
兩點,當直線![]() 的傾斜角互補時,試問:直線
的傾斜角互補時,試問:直線![]() 的斜率是否為定值;若是,請求出其定值;否則,請說明理由.
的斜率是否為定值;若是,請求出其定值;否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數![]() 與燒開一壺水所用時間
與燒開一壺水所用時間![]() 的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
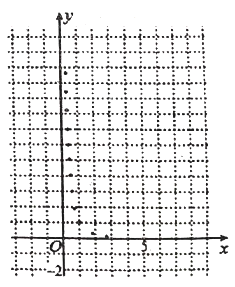
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作燒水時間
哪一個更適宜作燒水時間![]() 關于開關旋鈕旋轉的弧度數
關于開關旋鈕旋轉的弧度數![]() 的回歸方程類型?(不必說明理由)
的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)若單位時間內煤氣輸出量![]() 與旋轉的弧度數
與旋轉的弧度數![]() 成正比,那么,利用第(2)問求得的回歸方程知
成正比,那么,利用第(2)問求得的回歸方程知![]() 為多少時,燒開一壺水最省煤氣?
為多少時,燒開一壺水最省煤氣?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計值分別為
的斜率和截距的最小二乘法估計值分別為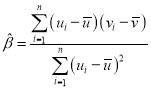 ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com