
【題目】已知雙曲線![]() 的漸近線方程為
的漸近線方程為![]() ,一個焦點為
,一個焦點為![]() .
.
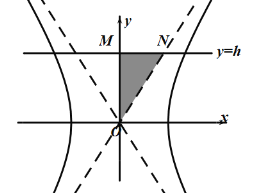
(1)求雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 上的任意一點
上的任意一點![]() ,分別作這兩條漸近線的平行線與這兩條漸近線得到四邊形
,分別作這兩條漸近線的平行線與這兩條漸近線得到四邊形![]() ,證明四邊形
,證明四邊形![]() 的面積是一個定值;
的面積是一個定值;
(3)設直線![]() 與
與![]()
![]() 在第一象限內與漸近線
在第一象限內與漸近線![]() 所圍成的三角形
所圍成的三角形![]() 繞著
繞著![]() 軸旋轉一周所得幾何體的體積.
軸旋轉一周所得幾何體的體積.
科目:高中數學 來源: 題型:
【題目】某工廠有甲,乙兩個車間生產同一種產品,,甲車間有工人![]() 人,乙車間有工人
人,乙車間有工人![]() 人,為比較兩個車間工人的生產效率,采用分層抽樣的方法抽取工人,甲車間抽取的工人記作第一組,乙車間抽取的工人記作第二組,并對他們中每位工人生產完成的一件產品的事件(單位:
人,為比較兩個車間工人的生產效率,采用分層抽樣的方法抽取工人,甲車間抽取的工人記作第一組,乙車間抽取的工人記作第二組,并對他們中每位工人生產完成的一件產品的事件(單位:![]() )進行統計,按照
)進行統計,按照![]() 進行分組,得到下列統計圖.
進行分組,得到下列統計圖.

![]() 分別估算兩個車間工人中,生產一件產品時間少于
分別估算兩個車間工人中,生產一件產品時間少于![]() 的人數
的人數
![]() 分別估計兩個車間工人生產一件產品時間的平均值,并推測車哪個車間工人的生產效率更高?
分別估計兩個車間工人生產一件產品時間的平均值,并推測車哪個車間工人的生產效率更高?
![]() 從第一組生產時間少于
從第一組生產時間少于![]() 的工人中隨機抽取
的工人中隨機抽取![]() 人,記抽取的生產時間少于
人,記抽取的生產時間少于![]() 的工人人數為隨機變量
的工人人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高速公路隧道設計為單向三車道,每條車道寬4米,要求通行車輛限高5米,隧道全長1.5千米,隧道的斷面輪廓線近似地看成半個橢圓形狀(如圖所示).

(1)若最大拱高![]() 為6米,則隧道設計的拱寬
為6米,則隧道設計的拱寬![]() 至少是多少米?(結果取整數)
至少是多少米?(結果取整數)
(2)如何設計拱高![]() 和拱寬
和拱寬![]() ,才能使半個橢圓形隧道的土方工程量最小?(結果取整數)
,才能使半個橢圓形隧道的土方工程量最小?(結果取整數)
參考數據:![]() ,橢圓的面積公式為
,橢圓的面積公式為![]() ,其中
,其中![]() ,
,![]() 分別為橢圓的長半軸和短半軸長.
分別為橢圓的長半軸和短半軸長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網絡營銷部門為了統計某市網友某日在某淘寶店的網購情況,隨機抽查了該市當天![]() 名網友的網購金額情況,得到如下統計表(如圖).
名網友的網購金額情況,得到如下統計表(如圖).
網購金額(單位:千元) | 頻數 | 頻率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若網購金額超過![]() 千元的顧客定義為“網購達人”,網購金額不超過
千元的顧客定義為“網購達人”,網購金額不超過![]() 千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為
千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為![]() .
.
(Ⅰ)試確定![]() 的值,并補全頻率分布直方圖(如圖);
的值,并補全頻率分布直方圖(如圖);
(Ⅱ)該營銷部門為了進一步了解這![]() 名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取
名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取![]() 人,若需從這
人,若需從這![]() 人中隨機選取
人中隨機選取![]() 人進行問卷調查.設
人進行問卷調查.設![]() 為選取的
為選取的![]() 人中“網購達人”的人數,求
人中“網購達人”的人數,求![]() 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線E:![]() 焦點F,過點F且斜率為2的直線與拋物線交于A、B兩點,且
焦點F,過點F且斜率為2的直線與拋物線交于A、B兩點,且![]() .
.
(1)求拋物線E的方程;
(2)設O是坐標原點,P,Q是拋物線E上分別位于x軸兩側的兩個動點,且![]()
①證明:直線PQ必過定點,并求出定點G的坐標;
②過G作PQ的垂線交拋物線于C,D兩點,求四邊形PCQD面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
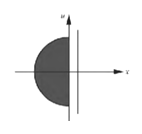
【題目】關于旋轉體的體積,有如下的古爾丁(guldin)定理:“平面上一區域D繞區域外一直線(區域D的每個點在直線的同側,含直線上)旋轉一周所得的旋轉體的體積,等于D的面積與D的幾何中心(也稱為重心)所經過的路程的乘積”.利用這一定理,可求得半圓盤 ,繞直線x
,繞直線x![]() 旋轉一周所形成的空間圖形的體積為_____.
旋轉一周所形成的空間圖形的體積為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
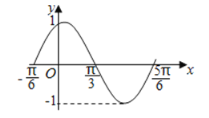
【題目】如圖是函數![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在區間
)在區間![]() 上的圖象,為了得到這個函數的圖象,只需將
上的圖象,為了得到這個函數的圖象,只需將![]() (
(![]() )的圖象上的所有的點( )
)的圖象上的所有的點( )
A. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
B. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
C. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
D. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com