
【題目】如圖,在三棱錐![]() 中,
中,![]() 是邊長為4的正三角形,
是邊長為4的正三角形, ![]() ,
,![]() 分別為
分別為![]() 的中點,且
的中點,且![]() .
.
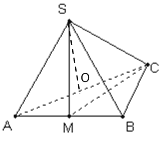
(1)證明:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
科目:高中數學 來源: 題型:
【題目】用數學歸納法證明1+2+3+…+n2= ![]() ,則當n=k+1時左端應在n=k的基礎上加上( )
,則當n=k+1時左端應在n=k的基礎上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數分布直方圖.這100名市民中,年齡不超過40歲的有65人將所抽樣本中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲. 
(1)根據已知條件完成下面的2×2列聯表,能否在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關?
網購迷 | 非網購迷 | 合計 | |
年齡不超過40歲 | |||
年齡超過40歲 | |||
合計 |
(2)若從網購迷中任意選取2名,求其中年齡丑啊過40歲的市民人數ξ的分布列與期望. 附: ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,直線l的參數方程為 ![]() (t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為 ![]() .
.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)求直線l被曲線C截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)= ![]() sin(2x+φ)(|φ|<
sin(2x+φ)(|φ|< ![]() )的圖象關于直線x=
)的圖象關于直線x= ![]() 對稱,且當x1 , x2∈(﹣
對稱,且當x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),x1≠x2時,f(x1)=f(x2),則f(x1+x2)等于( )
),x1≠x2時,f(x1)=f(x2),則f(x1+x2)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求CE與DB所成角的余弦值;
(Ⅱ)設點![]() 在線段
在線段![]() 上,且直線
上,且直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段
,求線段![]() 的長度
的長度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(cosx,
=(cosx, ![]() ),函數f(x)=(
),函數f(x)=( ![]() +
+ ![]() )
) ![]() .
.
(1)求函數f(x)的單調遞增區間;
(2)將函數f(x)的圖象向左平移 ![]() 個單位得到函數g(x)的圖象,在△ABC中,角A,B,C所對邊分別a,b,c,若a=3,g(
個單位得到函數g(x)的圖象,在△ABC中,角A,B,C所對邊分別a,b,c,若a=3,g( ![]() )=
)= ![]() ,sinB=cosA,求b的值.
,sinB=cosA,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省高考改革新方案,不分文理科,高考成績實行“3+3”的構成模式,第一個“3”是語文、數學、外語,每門滿分150分,第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試,每門滿分100分,高考錄取成績卷面總分滿分750分.為了調查學生對物理、化學、生物的選考情況,將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體S,從學生群體S中隨機抽取了50名學生進行調查,他們選考物理,化學,生物的科目數及人數統計如表:
選考物理、化學、生物的科目數 | 1 | 2 | 3 |
人數 | 5 | 25 | 20 |
(I)從所調查的50名學生中任選2名,求他們選考物理、化學、生物科目數量不相等的概率;
(II)從所調查的50名學生中任選2名,記X表示這2名學生選考物理、化學、生物的科目數量之差的絕對值,求隨機變量X的分布列和數學期望;
(III)將頻率視為概率,現從學生群體S中隨機抽取4名學生,記其中恰好選考物理、化學、生物中的兩科目的學生數記作Y,求事件“y≥2”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),設函數f(x)=
=(sin2x,n),設函數f(x)= ![]()
![]() ,且y=f(x)的圖象過點(
,且y=f(x)的圖象過點( ![]() ,
, ![]() )和點(
)和點( ![]() ,﹣2).
,﹣2).
(Ⅰ)求m,n的值;
(Ⅱ)將y=f(x)的圖象向左平移φ(0<φ<π)個單位后得到函數y=g(x)的圖象.若y=g(x)的圖象上各最高點到點(0,3)的距離的最小值為1,求y=g(x)的單調增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com