Question

13．某地方政府欲將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場，已知AD∥BC，AD⊥AB，AD=2BC=2$\sqrt{3}$百米，AB=3百米，廣場入口P在AB上，且AP=2BP，根據規劃，過點P鋪設兩條互相垂直的筆直小路PM、PN（小路寬度不計），點M、N分別在邊AD、BC上（包含端點），△PAM區域擬建為跳舞健身廣場，△PBN區域擬建為兒童樂園，其他區域鋪設綠化草坪，設∠APM=θ．
（1）求綠化草坪面積的最大值；
（2）現擬將兩條小路PN、PN進行不同風格的美化，小路PM的美化費用為每百米1萬元，小路PN的美化費用為每百米2萬元，試確定點M，N的位置，使得小路PM，PN的總美化費用最低，并求出最低費用．

Answer 1

分析 （1）用θ表示出AM，BN，得出草坪面積S關于tanθ的函數，利用函數單調性求出最大值；
（2）用θ表示出PM，PN，得出美化費用y關于θ的函數，利用換元法求出最小值．

解答 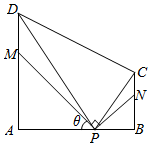解：（1）∵AB=3，AP=2BP，∴AP=2，BP=1．
在Rt△PMA中，由$\frac{AM}{AP}=tanθ$，得AM=2tanθ，
∴${S_{△PMA}}=\frac{1}{2}•2•2tanθ=2tanθ$，
∵PM⊥PN，∴∠PNB=θ，
在Rt△PNB中，由$\frac{BP}{BN}=tanθ$，得$BN=\frac{1}{tanθ}$，
所以${S_{△PMA}}=\frac{1}{2}•1•\frac{1}{tanθ}=\frac{1}{2tanθ}$，
又S_梯形ABCD=$\frac{1}{2}$（$\sqrt{3}$+2$\sqrt{3}$）×3=$\frac{9\sqrt{3}}{2}$．
∴綠化草坪面積S=$\frac{9\sqrt{3}}{2}$-2tanθ-$\frac{1}{2tanθ}$，
連結PC，PD，則tanθ的最大值為$\frac{AD}{AP}$=$\sqrt{3}$，tanθ的最小值為$\frac{BP}{BC}=\frac{\sqrt{3}}{3}$，
∴$\frac{\sqrt{3}}{3}$≤tanθ$≤\sqrt{3}$，
設tanθ=t，f（t）=2t+$\frac{1}{2t}$，則f′（t）=2-$\frac{1}{2{t}^{2}}$，
∴當t∈[$\frac{\sqrt{3}}{3}$，$\sqrt{3}$]時，f′（t）＞0，
∴f（t）在[$\frac{\sqrt{3}}{3}$，$\sqrt{3}$]上單調遞增，
∴f（t）的最小值為f（$\frac{\sqrt{3}}{3}$）=$\frac{7\sqrt{3}}{6}$，
∴S的最大值為$\frac{9\sqrt{3}}{2}$-$\frac{7\sqrt{3}}{6}$=$\frac{10\sqrt{3}}{3}$．
∴綠化草坪面積的最大值為$\frac{10\sqrt{3}}{3}$平方百米．
（2）在Rt△PMA中，由$\frac{AP}{PM}=cosθ$，得$PM=\frac{2}{cosθ}$，
在Rt△PNB中，由$\frac{BP}{PN}=sinθ$，得$PN=\frac{1}{sinθ}$，
∴總美化費用為$y=\frac{2}{cosθ}+\frac{2}{sinθ}=\frac{2（sinθ+cosθ）}{sinθcosθ}$，由（1）可知θ∈[$\frac{π}{6}$，$\frac{π}{3}$]，
令t=sinθ+cosθ=$\sqrt{2}$sin（θ+$\frac{π}{4}$），則t∈[$\frac{\sqrt{3}+1}{2}$，$\sqrt{2}$]，$sinθcosθ=\frac{{{t^2}-1}}{2}$，
∴$y=\frac{4t}{{{t^2}-1}}$，${y^'}=-\frac{{4{t^2}+4}}{{{{（{t^2}-1）}^2}}}＜0$，
∴$y=\frac{4t}{{{t^2}-1}}$在[$\frac{\sqrt{3}+1}{2}$，$\sqrt{2}$]上單調遞減，
∴當t=$\sqrt{2}$時，美化費用y取得最小值4$\sqrt{2}$．
∴當$t=\sqrt{2}$，即$θ=\frac{π}{4}$時，即AM=2，BM=1時總美化費用最低為4$\sqrt{2}$萬元．

點評 本題考查了函數解析式的求解，函數最值的計算，屬于中檔題．