
【題目】如圖,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.
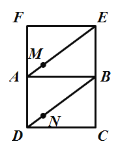
(1)求證:當(dāng)點(diǎn)F,A,D不共線時(shí),線段MN總平行于平面ADF.
(2)“不管怎樣翻折矩形ABEF,線段MN總與線段FD平行”這個(gè)結(jié)論正確嗎?如果正確,請(qǐng)證明;如果不正確,請(qǐng)說(shuō)明能否改變個(gè)別已知條件使上述結(jié)論成立,并給出理由.
【答案】(1)證明見(jiàn)解析;(2)這個(gè)結(jié)論不正確.要使上述結(jié)論成立,M,N應(yīng)分別為AE和DB的中點(diǎn),理由見(jiàn)解析
【解析】
(1)在平面圖形中,連接MN與AB交于點(diǎn)G,在平面圖形中可證![]() ,當(dāng)點(diǎn)F,A,D不共線時(shí),
,當(dāng)點(diǎn)F,A,D不共線時(shí),![]() ,
,![]() ,可證
,可證![]() 平面ADF,
平面ADF,![]() 平面ADF,從而有平面
平面ADF,從而有平面![]() 平面ADF,即可證明結(jié)論;
平面ADF,即可證明結(jié)論;
(2)這個(gè)結(jié)論不正確.要使上述結(jié)論成立,M,N應(yīng)分別為AE和DB的中點(diǎn).
當(dāng)點(diǎn)F,A,D共線時(shí),由(1)得![]() ;當(dāng)點(diǎn)F,A,D不共線時(shí),平面
;當(dāng)點(diǎn)F,A,D不共線時(shí),平面![]() 平面FDA,則要使
平面FDA,則要使![]() ,滿足FD與AN共面,只要FM與DN相交即可,可證交點(diǎn)只能為點(diǎn)B,得出只有M,N分別為AE,DB的中點(diǎn)才滿足.
,滿足FD與AN共面,只要FM與DN相交即可,可證交點(diǎn)只能為點(diǎn)B,得出只有M,N分別為AE,DB的中點(diǎn)才滿足.
(1)證明:在平面圖形中,連接MN,與AB交于點(diǎn)G.
∵四邊形ABCD和四邊形ABEF都是矩形,![]() ,
,
∴![]() 且
且![]() ,
,
∴四邊形ADBE是平行四邊形,∴![]() .
.
又![]() ,∴四邊形ADNM是平行四邊形,∴
,∴四邊形ADNM是平行四邊形,∴![]() .
.
當(dāng)點(diǎn)F,A,D不共線時(shí),如圖,![]() ,
,![]() ,
,

![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面ADF,
平面ADF,
同理![]() 平面ADF,又
平面ADF,又![]() ,
,
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面ADF.
平面ADF.
又![]() 平面GNM,∴
平面GNM,∴![]() 平面ADF.
平面ADF.
故當(dāng)點(diǎn)F,A,D不共線時(shí),線段MN總平行于平面FA D.
(2)解:這個(gè)結(jié)論不正確.
要使上述結(jié)論成立,M,N應(yīng)分別為AE和DB的中點(diǎn).理由如下:
當(dāng)點(diǎn)F,A,D共線時(shí),由(1)得![]() .
.
當(dāng)點(diǎn)F,A,D不共線時(shí),如圖,

由(1)知平面![]() 平面FDA,則要使
平面FDA,則要使![]() 總成立,
總成立,
根據(jù)面面平行的性質(zhì)定理,只要FD與![]() 共面即可.
共面即可.
若要使FD與![]() 共面,連接FM,只要FM與DN相交即可,
共面,連接FM,只要FM與DN相交即可,
∵![]() 平面ABEF,
平面ABEF,![]() 平面ABCD,
平面ABCD,
平面![]() 平面
平面![]() ,
,
∴若FM與DN相交,則交點(diǎn)只能為點(diǎn)B,
由于四邊形![]() 為平行四邊形,
為平行四邊形,![]() 與
與![]() 的交點(diǎn)
的交點(diǎn)![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),
則只有M,N分別為AE,DB的中點(diǎn)才滿足.
由![]() ,
,
可知它們確定一個(gè)平面,即F,D,N,M四點(diǎn)共面.
∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
平面![]() 平面FDA,∴
平面FDA,∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)證明:當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有最小值,設(shè)
有最小值,設(shè)![]() 最小值為
最小值為![]() ,求函數(shù)
,求函數(shù)![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 且
且![]() 是
是![]() 的導(dǎo)函數(shù),則過(guò)曲線
的導(dǎo)函數(shù),則過(guò)曲線![]() 上一點(diǎn)
上一點(diǎn)![]() 的切線方程為
的切線方程為![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,已知
中,已知![]() 側(cè)面
側(cè)面![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在棱
在棱![]() 上.
上.
(1)求![]() 的長(zhǎng),并證明
的長(zhǎng),并證明![]() 平面
平面![]() ;
;
(2)若![]() ,試確定
,試確定![]() 的值,使得
的值,使得![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】 如圖是正方體的平面展開(kāi)圖.在這個(gè)正方體中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四個(gè)命題中,正確命題的序號(hào)是________.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知三棱錐P-ABC,D,E,F(xiàn)分別是棱PA,PB,PC的中點(diǎn).求證:平面DEF∥平面ABC.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】程大位是明代著名數(shù)學(xué)家,他的《新編直指算法統(tǒng)宗》是中國(guó)歷史上一部影響巨大的著作,它問(wèn)世后不久便風(fēng)行宇內(nèi),成為明清之際研習(xí)數(shù)學(xué)者必讀的教材,而且傳到朝鮮、日本及東南亞地區(qū),對(duì)推動(dòng)漢字文化圈的數(shù)學(xué)發(fā)展起了重要的作用.卷八中第33問(wèn)是:“今有三角果一垛,底闊每面七個(gè),問(wèn)該若干?”如圖是解決該問(wèn)題的程序框圖,執(zhí)行該程序框圖,求得該垛果子的總數(shù)![]() 為( )
為( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,側(cè)面
中,側(cè)面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
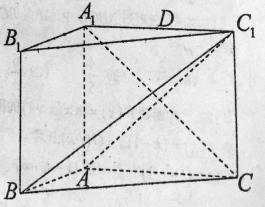
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設(shè)![]() 是
是![]() 的中點(diǎn),判斷并證明在線段
的中點(diǎn),判斷并證明在線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使
,使![]() 平面
平面![]() ,若存在,求點(diǎn)
,若存在,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com