Question

【題目】如圖，在三棱柱中，側面是矩形，，，，且.

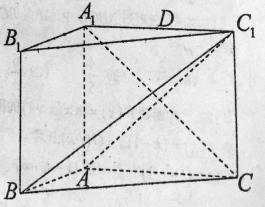
（1）求證：平面平面；

（2）設是的中點，判斷并證明在線段上是否存在點，使平面，若存在，求點到平面的距離.

Answer 1

【答案】(1)證明見解析；(2)為的中點，.

【解析】

試題分析：(1)借助題設條件運用面面垂直的判定定理推證；(2)借助題設運用線面平行的判定定理及等積法探求.

試題解析：

（1）在三棱柱中，側面是矩形，

又，，

平面，

，又，，

又，，

平面，又平面，

平面平面………………………………………6分

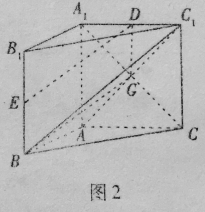
（2）解法一：當為的中點時，連接，

如圖1，取的中點，連接，

，，

又，，

所以平面平面，又平面，

平面，

又因為，平面，

設點到平面的距離為，

，，

所以點到平面的距離為.…………………………………12分

解法2.當為的中點時，連接，如圖2，設交于點，連接，

且，

四邊形為平行四邊形，則，又平面，平面，

平面，

求距離同解法一.