
【題目】某玩具生產公司每天計劃生產衛兵、騎兵、傘兵這三種玩具共100個,生產一個衛兵需5分鐘,生產一個騎兵需7分鐘,生產一個傘兵需4分鐘,已知總生產時間不超過10小時,若生產一個衛兵可獲利潤5元,生產一個騎兵可獲利潤6元,生產一個傘兵可獲利潤3元.
(1)用每天生產的衛兵個數![]() 與騎兵個數
與騎兵個數![]() 表示每天的利潤
表示每天的利潤![]() (元);
(元);
(2)怎樣分配生產任務才能使每天的利潤最大,最大利潤是多少?
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,且過點(1,
,且過點(1,![]() ).
).
(I)求橢圓C的方程;
(Ⅱ)設與圓O:x2+y2=![]() 相切的直線l交橢圓C與A,B兩點,求△OAB面積的最大值,及取得最大值時直線l的方程.
相切的直線l交橢圓C與A,B兩點,求△OAB面積的最大值,及取得最大值時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有兩枚大小相同、質地均勻的正四面體玩具,每個玩具的各個面上上分別寫著數字1,2,3,5,同時投擲這兩枚玩具一次,記![]() 為兩個朝下的面上的數字之和.
為兩個朝下的面上的數字之和.
(1)求事件“![]() 不小于6”的概率;
不小于6”的概率;
(2)“![]() 為奇數”的概率和“
為奇數”的概率和“![]() 為偶數”的概率是不是相等?證明你作出的結論.
為偶數”的概率是不是相等?證明你作出的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)直線![]() 過
過![]() 且與曲線
且與曲線![]() 相切,求直線
相切,求直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 與點
與點![]() 關于
關于![]() 軸對稱,求曲線
軸對稱,求曲線 ![]() 上的點到點
上的點到點![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,橢圓
,橢圓![]() 過點
過點 ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,且
,且![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是橢圓
是橢圓![]() 的上頂點,過點
的上頂點,過點![]() 分別作直線
分別作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,設這兩條直線的斜率分別為
兩點,設這兩條直線的斜率分別為![]() ,且
,且![]() ,證明:直線
,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側面
中,側面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
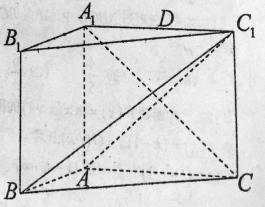
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 是
是![]() 的中點,判斷并證明在線段
的中點,判斷并證明在線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,求點
,若存在,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個不透明的盒子中,放有標號分別為![]() ,
,![]() ,
,![]() ,
,![]() 的四個大小相同的小球,現從這個盒子中,有放回地先后取得兩個小球,其標號分別為
的四個大小相同的小球,現從這個盒子中,有放回地先后取得兩個小球,其標號分別為![]() ,
,![]() .
.
(1)求事件![]() 的概率;
的概率;
(2)求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌茶壺的原售價為80元一個,今有甲、乙兩家茶具店銷售這種茶壺,甲店用如下的方法促銷:如果只購買一只茶壺,其價格為78元/個;如果一次購買兩個茶壺,其價格為76元/個;…;如果一次購買的茶壺數每增加一個,那么茶壺的價格減少2元/個,但茶壺的售價不得低于44元/個。乙店一律按原價的75%銷售。現某茶社要購買這種茶壺![]() 個,如果全部在甲店購買,則所需金額為
個,如果全部在甲店購買,則所需金額為![]() 元;如果全部在乙店購買,則所需金額為
元;如果全部在乙店購買,則所需金額為![]() 元。
元。
(1)分別求出![]() 、
、![]() 與
與![]() 之間的函數關系式。
之間的函數關系式。
(2)該茶社去哪家茶具店購買茶壺花費較少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人參加微信群搶紅包游戲,規則如下:每輪游戲發![]() 個紅包,每個紅包金額為
個紅包,每個紅包金額為![]() 元,
元,![]() .已知在每輪游戲中所產生的
.已知在每輪游戲中所產生的![]() 個紅包金額的頻率分布直方圖如圖所示.
個紅包金額的頻率分布直方圖如圖所示.
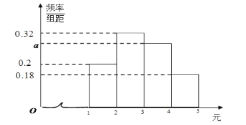
(1)求![]() 的值,并根據頻率分布直方圖,估計紅包金額的眾數;
的值,并根據頻率分布直方圖,估計紅包金額的眾數;
(2)以頻率分布直方圖中的頻率作為概率,若甲、乙、丙三人從中各搶到一個紅包,其中金額在![]() 的紅包個數為
的紅包個數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com