
【題目】已知函數![]()
(Ⅰ)討論![]() 的單調性;
的單調性;
(Ⅱ)若![]() 有兩個零點,求
有兩個零點,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)對函數![]() 求導,討論當
求導,討論當![]() 時,
時,![]() 時,
時,![]() 時,
時,![]() 時,由導數大于0,可得增區間,由導數小于0,可得減區間;(Ⅱ)由(Ⅰ)的單調區間,對
時,由導數大于0,可得增區間,由導數小于0,可得減區間;(Ⅱ)由(Ⅰ)的單調區間,對![]() 討論,結合單調性和函數值的變化特點,即可得到所求范圍.
討論,結合單調性和函數值的變化特點,即可得到所求范圍.
(Ⅰ)由題![]() ,
,
(1)當![]() 時,
時,![]() 故
故![]() 時,
時,![]() 函數
函數![]() 單調遞減,
單調遞減,![]() 時,
時,![]() 函數
函數![]() 單調遞增;
單調遞增;
(2)當![]() 時,故
時,故![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,
單調遞增,![]() 時,
時,![]() ,函數
,函數![]() 單調遞減,
單調遞減,![]() 時,
時,![]() ,函數
,函數![]() 單調遞增;
單調遞增;
(3)當![]() 時,
時,![]() 恒成立,函數
恒成立,函數![]() 單調遞增;
單調遞增;
(4)當![]() 時,故
時,故![]() 時,
時,![]() 函數
函數![]() 單調遞增,
單調遞增,
![]() 時,
時,![]() 函數
函數![]() 單調遞減,
單調遞減,
![]() 時,
時,![]() 函數
函數![]() 單調遞增;
單調遞增;
(Ⅱ)當![]() 時,
時,![]() 有唯一零點
有唯一零點![]() 不符合題意;
不符合題意;
由(Ⅰ)知:當![]() 時,故
時,故![]() 時,函數
時,函數![]() 單調遞減,
單調遞減,![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,
,![]() 必有兩個零點;
必有兩個零點;
當![]() 時,故
時,故![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,
![]() 時,函數
時,函數![]() 單調遞減,
單調遞減,![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,![]() ,函數
,函數![]() 至多有一個零點;
至多有一個零點;
當![]() 時,函數
時,函數![]() 單調遞增,函數
單調遞增,函數![]() 至多有一個零點;
至多有一個零點;
當![]() 時,故
時,故![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,![]() 時,函數
時,函數![]() 單調遞減,
單調遞減,![]() 時,函數
時,函數![]() 單調遞增,
單調遞增,![]() ,函數
,函數![]() 至多有一個零點;
至多有一個零點;
綜上所述:當![]() 時,函數
時,函數![]() 有兩個零點.
有兩個零點.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意x,y∈R,總有f(x)+f(y)=f(x+y),且當x>0時,f(x)<0,f(1)=-![]() .
.
(1)求證:f(x)是R上的單調減函數.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】江蘇省淮陰中學科技興趣小組在計算機上模擬航天器變軌返回試驗.設計方案如圖,航天器運行(按順時針方向)的軌跡方程為![]() ,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以
,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以![]() 軸為對稱軸、
軸為對稱軸、![]() 為頂點的拋物線的實線部分,降落點為
為頂點的拋物線的實線部分,降落點為![]() .觀測點
.觀測點![]() 同時跟蹤航天器,試問:當航天器在
同時跟蹤航天器,試問:當航天器在![]() 軸上方時,觀測點
軸上方時,觀測點![]() ,
,![]() 測得離航天器的距離分別為多少時,應向航天器發出變軌指令?(變軌指令發出時航天器立即變軌)。
測得離航天器的距離分別為多少時,應向航天器發出變軌指令?(變軌指令發出時航天器立即變軌)。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,且相鄰兩對稱軸間的距離為
為奇函數,且相鄰兩對稱軸間的距離為![]()
(1)當![]() 時,求
時,求![]() 的單調遞減區間;
的單調遞減區間;
(2)將函數![]() 的圖象沿
的圖象沿![]() 軸正方向向右平移
軸正方向向右平移![]() 個單位長度,再把橫坐標縮短為原來的
個單位長度,再把橫坐標縮短為原來的![]() (縱坐標不變),得到函數
(縱坐標不變),得到函數![]() 的圖象,當
的圖象,當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.
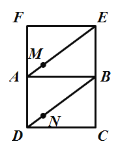
(1)求證:當點F,A,D不共線時,線段MN總平行于平面ADF.
(2)“不管怎樣翻折矩形ABEF,線段MN總與線段FD平行”這個結論正確嗎?如果正確,請證明;如果不正確,請說明能否改變個別已知條件使上述結論成立,并給出理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() +xlnx,g(x)=x3﹣x2﹣3.
+xlnx,g(x)=x3﹣x2﹣3.
(1)討論函數h(x)=![]() 的單調性;
的單調性;
(2)如果對任意的s,t∈[![]() ,2],都有f(s)≥g(t)成立,求實數a的取值范圍.
,2],都有f(s)≥g(t)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知袋子中放有大小和形狀相同的小球若干,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球![]() 個.若從袋子中隨機抽取1個小球,取到標號為2的小球的概率是
個.若從袋子中隨機抽取1個小球,取到標號為2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)從袋子中不放回地隨機抽取2個小球,記第一次取出的小球標號為![]() ,第二次取出的小球標號為
,第二次取出的小球標號為![]() .記“
.記“![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com