【題目】動點
從坐標(biāo)原點
出發(fā)沿著拋物線
移動到點
，則在移動過程中當(dāng)
為最大時，
點的橫坐標(biāo)
________.
【答案】
【解析】
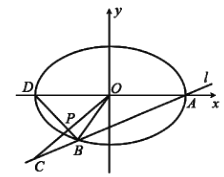
如圖所示，以
和
為兩個焦點作一個橢圓與
弧段（拋物線弧段）相切于
點（弧段整個地包含于橢圓內(nèi)部或邊界上.若有幾個切點，則任取其中一點）.由橢圓的定義可推知：橢圓內(nèi)部的點到兩個焦點的距離之和小于橢圓上的點到兩個焦點的距離之和（用三角形兩邊之和大于第三邊易證），所以，對弧段上任意一點
，必有
，即
就是最大值.下面求點的橫坐標(biāo).
過點作橢圓和拋物線的公切線
，則由橢圓的光學(xué)反射性質(zhì)知：
和
與的夾角相等.設(shè)點的坐標(biāo)為
，則的斜率為
（參見第一試第五題的題注），的斜率為
，而的斜率為
.由兩直線間的夾角公式得
，化簡得 
.
配方得 
.取其正根得
.綜合上述知，當(dāng)
為最大時，點橫坐標(biāo)
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知點
是橢圓
的右焦點，點
，
分別是
軸，
軸上的動點，且滿足
.若點
滿足
（
為坐標(biāo)原點）．
（Ⅰ）求點的軌跡
的方程；
（Ⅱ）設(shè)過點任作一直線與點的軌跡交于
，
兩點，直線
，
與直線
分別交于點
，
，試判斷以線段
為直徑的圓是否經(jīng)過點？請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
，且經(jīng)過點
.
求橢圓的標(biāo)準(zhǔn)方程；
設(shè)
為橢圓的中線，點
，過點
的動直線
交橢圓于另一點
，直線上的點滿足
，求直線
與
的交點
的軌跡方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題中正確的是（ ）
A. 命題
：
，
，則命題
：
，
B. “
”是“
”的充要條件
C. 命題“若
，則
或
”的逆否命題是“若
或
，則
”
D. 命題：，
；命題
：對，總有
；則
是真命題
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
,
（1）若關(guān)于
的不等式
的解集為
，求實數(shù)
的值；
（2）求不等式的解集；
（3）若對于
，
恒成立，求實數(shù)的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】2019年，隨著中國第一款5G手機投入市場，5G技術(shù)已經(jīng)進入高速發(fā)展階段.已知某5G手機生產(chǎn)廠家通過數(shù)據(jù)分析，得到如下規(guī)律：每生產(chǎn)手機
萬臺，其總成本為
，其中固定成本為800萬元，并且每生產(chǎn)1萬臺的生產(chǎn)成本為1000萬元（總成本=固定成本+生產(chǎn)成本），銷售收入
萬元滿足
（1）將利潤
表示為產(chǎn)量
萬臺的函數(shù)；
（2）當(dāng)產(chǎn)量為何值時，公司所獲利潤最大？最大利潤為多少萬元？
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
