
分析 (1)a=1時,化簡函數f(x),根據二次函數和三角函數的性質即可求出f(x)的最大、最小值與對應的x的值;
(2)化簡函數f(x),討論a的取值范圍,利用二次函數的圖象與性質,即可求出f(x)的最大值.
解答 解:(1)a=1時,函數f(x)=sin2x+cosx+5
=1-cos2x+cosx+5
=-${(cosx-\frac{1}{2})}^{2}$+$\frac{25}{4}$,
當cosx=$\frac{1}{2}$,即x=2kπ±$\frac{π}{3}$,k∈Z時,
函數f(x)取得最大值$\frac{25}{4}$,
當cosx=-1,即x=2kπ+π,k∈Z時,
函數f(x)取得最小值4;
(2)函數f(x)=sin2x+acosx+5
=1-cos2x+acosx+5
=-${(cosx-\frac{a}{2})}^{2}$+6+$\frac{{a}^{2}}{4}$,a∈R;
當a≤-2,即$\frac{a}{2}$≤-1時,f(x)在cosx=-1時取得最大值5-a;
當-2<a<2,即-1<$\frac{a}{2}$<1時,f(x)在cosx=$\frac{a}{2}$時取得最大值6+$\frac{{a}^{2}}{4}$;
當a≥2,即$\frac{a}{2}$≥1時,f(x)在cos=1時取得最大值5+a;
∴函數f(x)在R上的最大值為
g(a)=$\left\{\begin{array}{l}{5-a,a≤-2}\\{6+\frac{{a}^{2}}{4},-2<a<2}\\{5+a,a≥2}\end{array}\right.$.
點評 本題考查了三角函數的圖象與性質的應用問題,也考查了二次函數的圖象與性質的應用問題,是綜合性題目.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | l1一定與l4垂直 | |
| B. | l1一定與l4平行 | |
| C. | l1一定與l4共面 | |
| D. | l1與l4的位置關系可能是平行,相交,或異面 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
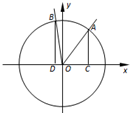 在平面直角坐標系xOy中,角α的頂點是坐標原點,始邊為x軸的正半軸,終邊與單位圓O交于點A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).將角α終邊繞原點按逆時針方向旋轉$\frac{π}{4}$,交單位圓于點B(x2,y2).過A,B作x軸的垂線,垂足分別為C,D,記△AOC及△BOD的面積分別為S1,S2,且S1=$\frac{4}{3}$S2,則tanα的值等于( )
在平面直角坐標系xOy中,角α的頂點是坐標原點,始邊為x軸的正半軸,終邊與單位圓O交于點A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).將角α終邊繞原點按逆時針方向旋轉$\frac{π}{4}$,交單位圓于點B(x2,y2).過A,B作x軸的垂線,垂足分別為C,D,記△AOC及△BOD的面積分別為S1,S2,且S1=$\frac{4}{3}$S2,則tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{4}{21}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
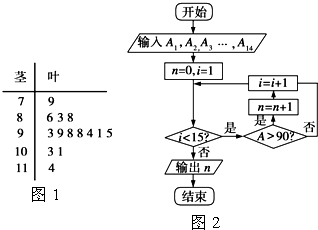 如圖1是某高三學生進入高中-二年來的數學考試成績莖葉圖,第1次到第 14次.考試成績依次記為A1,A2,…,A14.如圖2是統計莖葉圖中成績在一定范圍內考試次數的一個算法流程圖.那么算法流程圖輸出的結果是10.
如圖1是某高三學生進入高中-二年來的數學考試成績莖葉圖,第1次到第 14次.考試成績依次記為A1,A2,…,A14.如圖2是統計莖葉圖中成績在一定范圍內考試次數的一個算法流程圖.那么算法流程圖輸出的結果是10.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=3cosx | B. | f(x)=x3+x2 | C. | f(x)=1+sin2x | D. | f(x)=ex+x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com