
分析 (1)由f(-x)+f(x)=ex+e-x,可判斷f(x)=ex+x3是“e函數”;
(2)若f(x)為“e函數”且$f(x)-f(-x)={e^x}-{e^{-x}}-\frac{2}{x}$,
(ⅰ)由于y=ex與$y=-\frac{1}{x}$均為增函數,可知f(x)在(0,+∞)上為增函數,通過計算知f($\frac{1}{2}$)=$\sqrt{e}$-2<0,f(2)=e2-$\frac{1}{2}$>0,利用零點存在定理即可證得:f(x)的零點在$(\frac{1}{2},2)$上;
(ⅱ)由(ⅰ)知,f(x)的零點x0∈($\frac{1}{2}$,2),且f(x0)=0,從而可證:對任意a>0,存在λ>0,使f(x)<0在(0,λa)上恒成立.
解答 (1)解:∵f(-x)+f(x)=e-x-x3+ex+x3=ex+e-x,
∴f(x)為“e函數”.
(2)證明:∵f(-x)+f(x)=ex+e-x①,
$f(x)-f(-x)={e^x}-{e^{-x}}-\frac{2}{x}$②
∴①+②得:$2f(x)=2{e^x}-\frac{2}{x}$,∴$f(x)={e^x}-\frac{1}{x}$.
(ⅰ)∵y=ex與$y=-\frac{1}{x}$均為增函數,∴f(x)在(0,+∞)上為贈函數,
又ex>0,∴f(x)的唯一零點必在(0,+∞)上.
∵f($\frac{1}{2}$)=${e}^{\frac{1}{2}}$-2=$\sqrt{e}$-2<0,f(2)=e2-$\frac{1}{2}$>0,
∴f(x)的唯一零點在($\frac{1}{2}$,2)上.
(ⅱ)由(ⅰ)知,f(x)的零點x0∈($\frac{1}{2}$,2),且f(x0)=0,
又f(x)在(0,+∞)上為增函數,∴f(x)<0在(0,x0)上恒成立,
∴對任意a>0,存在λ=$\frac{{x}_{0}}{a}$>0,使f(x)<0在(0,λa)上恒成立.
點評 本題考查函數恒成立問題,考查函數單調性、零點存在定理的應用,考查運算推理能力,屬于難題.


科目:高中數學 來源: 題型:選擇題
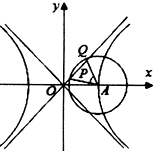 如圖,已知雙曲線$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右頂點為A,O為坐標原點,以A為圓心的圓與雙曲線C的某漸近線交于兩點P、Q,若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,則雙曲線C的離心率為( )
如圖,已知雙曲線$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右頂點為A,O為坐標原點,以A為圓心的圓與雙曲線C的某漸近線交于兩點P、Q,若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,則雙曲線C的離心率為( )| A. | $\frac{{2\sqrt{13}}}{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\frac{{2\sqrt{39}}}{9}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com