
分析 (1)由已知可$\overrightarrow{m}•\overrightarrow{n}$=0,進而由同角三角函數基本關系式可得cosA=$\frac{1}{2}$,結合A的范圍,進而得到∠A的大小;
(2)由已知利用三角形面積公式可求bc=12,利用余弦定理可求b2+c2=25,聯立即可解得b,c的值.
解答 解:(1)∵$\overrightarrow{m}⊥\overrightarrow{n}$,$\overrightarrow{m}$=(tanA+tanB,-tanB),$\overrightarrow{n}$=(b,2c),
∴$\overrightarrow{m}•\overrightarrow{n}$=0,可得:b(tanA+tanB)-2ctanB=0,
∴$\frac{sinBsinC}{cosAcosB}$=$\frac{2sinBsinC}{cosB}$,可得:cosA=$\frac{1}{2}$,
又∵A∈(0,π),
∴A=$\frac{π}{3}$.
(2)∵S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×bc×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴bc=12,①
又∵a2=b2+c2-2bccosA=b2+c2-bc=b2+c2-12=13,可得:b2+c2=25,②
∴聯立①②解得:$\left\{\begin{array}{l}{b=3}\\{c=4}\end{array}\right.$,或$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$.
點評 本題主要考查了平面向量數量積的坐標運算,同角三角函數基本關系式,三角形面積公式,余弦定理在解三角形中的綜合應用,考查了轉化思想,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
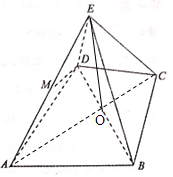 如圖幾何體E-ABCD是四棱錐,△ABD為正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,
如圖幾何體E-ABCD是四棱錐,△ABD為正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3 個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
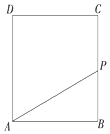 如圖所示,動點P從邊長為1的正方形ABCD的頂點A出發,順次經過頂點B,C,D再回到A.設x表示P點的路程,y表示PA的長度,求y關于x的函數關系式.
如圖所示,動點P從邊長為1的正方形ABCD的頂點A出發,順次經過頂點B,C,D再回到A.設x表示P點的路程,y表示PA的長度,求y關于x的函數關系式.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
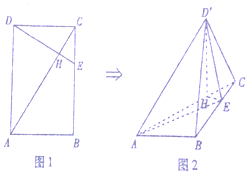 如圖1,已知矩形ABCD中,點E是邊BC上的點,DE與AC相交于點H,且CE=1,AB=$\sqrt{3}$,BC=3,現將△ACD沿AC折起,如圖2,點D的位置記為D′,此時ED′=$\frac{\sqrt{10}}{2}$
如圖1,已知矩形ABCD中,點E是邊BC上的點,DE與AC相交于點H,且CE=1,AB=$\sqrt{3}$,BC=3,現將△ACD沿AC折起,如圖2,點D的位置記為D′,此時ED′=$\frac{\sqrt{10}}{2}$查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
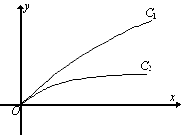 如圖,當參數λ=λ1,λ2時,連續函數y=$\frac{x}{1+λx}$(x≥0)的圖象分別對應曲線C1和C2,則( )
如圖,當參數λ=λ1,λ2時,連續函數y=$\frac{x}{1+λx}$(x≥0)的圖象分別對應曲線C1和C2,則( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com