Question

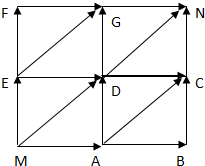
16．某商店老板設計了如下有獎游戲方案：顧客只要花10元錢，即可參加有獎游戲一次．游戲規則如下：棋子從點M開始沿箭頭方向跳向N，每次只跳一步（即一個箭頭），當下一步有方向選擇時，跳的方法必須通過投擲骰子決定，方案如下：當擲出的點數為1時，沿$\overrightarrow{MD}$方向跳一步；當擲出的點數為2，4，6時，沿$\overrightarrow{ME}$方向跳一步；當擲出的點數為3，5時，沿$\overrightarrow{MA}$方向跳一步；獎勵標準如表：

從M到N用的步數	2	3	4
獎勵金額（元）	100	10	5

若該店平均每天有200人參加游戲，按每月30天計算．則該店開展此游戲每月獲利的期望（均值）為2083元
（精確到1元）

Answer 1

分析 根據游戲規則得到ξ分布列．分類討論：當ξ=-90和ξ=0時P的值，則易得Eξ=-90×$\frac{1}{36}$+5×$\frac{23}{36}$=$\frac{25}{36}$（元），故小商店每月獲利大約有$\frac{25}{36}$×100×30．

解答 解：設一位顧客參加一次游戲后，小商店獲利為ξ元，則ξ分布列為：

ξ	-90	0	5
從M到N所用步數	2	3	4
P	P1	P2	P3

當ξ=-90時，只有一種跳棋路線M→D→N
P₁=$\frac{1}{6}$×$\frac{1}{6}$=$\frac{1}{36}$
當ξ=0，有如下跳棋路線
M→D→C→N   M→D→C→N    M→A→D→N
M→E→D→N   M→A→C→N    M→E→C→N
∴P₂=（$\frac{1}{6}$×$\frac{2}{6}$）+（$\frac{1}{6}$×$\frac{3}{6}$）+（$\frac{1}{6}$×$\frac{3}{6}$×$\frac{2}{6}$）+（$\frac{3}{6}$×$\frac{2}{6}$×$\frac{1}{6}$）+（$\frac{2}{6}$×$\frac{1}{6}$）+（$\frac{3}{6}$×$\frac{1}{6}$）=$\frac{1}{3}$
∴P₃=1-$\frac{1}{36}$_-$\frac{1}{3}$=$\frac{23}{36}$
∴Eξ=-90×$\frac{1}{36}$+5×$\frac{23}{36}$=$\frac{25}{36}$（元）
∴小商店每月獲利大約有$\frac{25}{36}$×100×30=$\frac{6250}{3}$≈2 083（元）．
故答案是：2083．

點評 本題考查了離散型隨機變量的期望與方差．考查計算能力，屬于中檔題．