
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
分析 由導數性質推導出當x∈(-∞,0)或x∈(0,+∞)時,函數y=xf(x)單調遞減.由此能求出結果.
解答 解∵函數y=f(x-1)的圖象關于直線x=1對稱,
∴y=f(x)關于y軸對稱,
∴函數y=xf(x)為奇函數.
∵[xf(x)]'=f(x)+xf'(x),
∴當x∈(-∞,0)時,[xf(x)]'=f(x)+xf'(x)<0,函數y=xf(x)單調遞減,
當x∈(0,+∞)時,函數y=xf(x)單調遞減.
∵$0<sin\frac{1}{2}<\frac{1}{2}$,
$1>ln2>ln\sqrt{e}=\frac{1}{2}$,
${log_{\frac{1}{2}}}\frac{1}{4}=2$$0<sin\frac{1}{2}<ln2<{log_{\frac{1}{2}}}\frac{1}{4}$,
∴a>b>c,
故選:A.
點評 本題考查三個數的大小的比較,解題時要認真審題,注意導數性質、函數性質的合理運用,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若命題p為真命題,命題q為假命題,則命題“p∨(¬q)”為真命題 | |
| B. | 命題“若a+b≠7,則a≠2或b≠5”為真命題 | |
| C. | 命題“若x2-x=0,則x=0或x=1”的否命題為“若x2-x=0,則x≠0且x≠1” | |
| D. | 命題p:?x>0,sinx>2x-1,則¬p為?x>0,sinx≤2x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
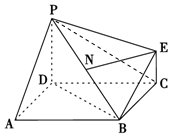 如圖為一簡單組合體,其底面ABCD為正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N為線段PB的中點.
如圖為一簡單組合體,其底面ABCD為正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N為線段PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分但非必要條件 | B. | 必要但非充分條件 | ||
| C. | 充要條件 | D. | 既非充分也非必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com