
分析 (1)若f(x)為偶函數,則b=0此時g(x)=$\frac{-1}{{a}^{2}x}$滿足g(-x)=-g(x)為奇函數;
(2)①由g(x)=x得有不等實根,整理后得一二次方程,故可得△>0,其為一關于a,b的關系式,從中整理 得出對稱軸的范圍,知其不在區間(-1,1)上,故可證得函數在區間(-1,1)上具有單調性.
②方程f(x)=0為一二次函數其兩實根為x3,x4(x3<x4),若x3<x1<x2<x4成立,即x1,x2在兩根之間,可由根的分布的相關知識將這一關系轉化為不等式,解出a的范圍
解答 解:(1)若f(x)為偶函數,則f(-x)=f(x),
即ax2-bx+1=ax2+bx+1,解得:b=0,
此時g(x)=$\frac{-1}{{a}^{2}x}$滿足g(-x)=-g(x),
即g(x)為奇函數;(4分)
(2)①由g(x)=x得方程a2x2+bx+1=0(*)有不等實根
∴△=b2-4a2>0及a≠0得|-$\frac{b}{2a}$|>1即-$\frac{b}{2a}$<-1或-$\frac{b}{2a}$>1(7分)
又f(x)的對稱軸x=-$\frac{b}{2a}$∉(-1,1)
故f(x)在(-1,1)上是單調函數(10分)
②x1,x2是方程(*)的根,∴a2x12+bx1+1=0
∴bx1=-a2x12-1,同理bx2=-a2x22-1
∴f(x1)=ax12+bx1+1=ax12-a2x12=(a-a2)x12
同理f(x2)=(a-a2)x22
要使x3<x1<x2<x4,只需$\left\{\begin{array}{l}a>0\\ f({x}_{1})<0\\ f({x}_{2})<0\end{array}\right.$,
即 $\left\{\begin{array}{l}a>0\\ a-{a}^{2}<0\end{array}\right.$,∴a>1
或$\left\{\begin{array}{l}a<0\\ f({x}_{1})>0\\ f({x}_{2})>0\end{array}\right.$,
即$\left\{\begin{array}{l}a<0\\ a-{a}^{2}>0\end{array}\right.$,解集為φ
故a的取值范圍a>1(16分)
點評 本題考查的知識點是二次函數的圖象和性質,熟練掌握二次函數的圖象和性質,是解答的關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
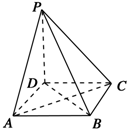 如圖所示,在四棱錐P-ABCD中,底面是邊長為a的正方形,側棱PD=a,PA=PC=$\sqrt{2}$a,
如圖所示,在四棱錐P-ABCD中,底面是邊長為a的正方形,側棱PD=a,PA=PC=$\sqrt{2}$a,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{4\sqrt{10}}}{5}$ | D. | $\frac{{8\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a≤$\frac{41}{8}$ | B. | a≤11 | C. | a≥$\frac{41}{8}$ | D. | a≥11 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com