
【題目】若函數![]()
![]() 在其定義域內有兩個不同的極值點.
在其定義域內有兩個不同的極值點.
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)試比較![]() 與
與![]() 的大小,并說明理由;
的大小,并說明理由;
(3)設![]() 的兩個極值點為
的兩個極值點為![]() ,
,![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
(1) 求函數的導數,利用![]() 在
在![]() 有兩個不同根,轉化為函數
有兩個不同根,轉化為函數![]() 與函數
與函數![]() 的圖象在
的圖象在![]() 上有兩個不同交點,從而
上有兩個不同交點,從而![]() 極大值
極大值![]() ,利用數形結合所以要想函數
,利用數形結合所以要想函數![]() 與函數
與函數![]() 的圖象在
的圖象在![]() 上有兩個不同交點,只需
上有兩個不同交點,只需![]() ,可得
,可得![]() 的取值范圍;
的取值范圍;
(2)由(1)利用![]() 在
在![]() 上單調性質可得試比較
上單調性質可得試比較![]() 與
與![]() 的大小;
的大小;
(3)證明![]() 等價于證明
等價于證明![]() ,
,
令![]() ,則
,則![]() ,等價于
,等價于![]() 的最小值大于0即可.
的最小值大于0即可.
解:(1)由已知![]() 得函數定義域為
得函數定義域為![]() ,
,
則![]() 在
在![]() 有兩個不同的根,
有兩個不同的根,
又![]() ,
,
即方程![]() 在
在![]() 上有兩個不同的根,
上有兩個不同的根,
轉化為函數![]() 與函數
與函數![]() 的圖像在
的圖像在![]() 上有兩個不同的交點,
上有兩個不同的交點,
又![]() ,
,
即![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
從而![]() ,
,
又![]() 有且只有一個零點是1,且在
有且只有一個零點是1,且在![]() 時,
時,![]() ,在
,在![]() 時,
時,![]() ,
,
所以要想函數![]() 與函數
與函數![]() 的圖像在
的圖像在![]() 上有兩個不同的交點,
上有兩個不同的交點,
只需![]() ,
,
即![]() ;
;
(2)由(1)![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() ,即
,即![]() ,
,
即![]() ,
,
即![]() ,
,
所以![]() ;
;
(3)設![]() 的兩個極值點為
的兩個極值點為![]() ,由(1)可知
,由(1)可知![]() 分別是方程
分別是方程![]() 的兩個根,
的兩個根,
即![]() ,
,
設![]() ,作差得,
,作差得,
![]() ,即
,即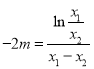 ,
,
要證明不等式![]() ,即等價于證明
,即等價于證明
![]() ,
,
令![]() ,則
,則![]() ,
,
![]() ,
,
設![]() ,
,
![]() ,
,
則函數![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
即不等式![]() 成立,
成立,
故所證不等式![]() 成立.
成立.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案科目:高中數學 來源: 題型:
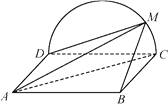
【題目】如圖,邊長為2的正方形![]() 所在的平面與半圓弧
所在的平面與半圓弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的點.
的點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 體積最大時,求面
體積最大時,求面![]() 與面
與面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,動點
,動點![]() 與
與![]() 、
、![]() 兩點連線的斜率之積為
兩點連線的斜率之積為![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知點![]() 是軌跡
是軌跡![]() 上的動點,點
上的動點,點![]() 在直線
在直線![]() 上,且滿足
上,且滿足![]() (其中
(其中![]() 為坐標原點),求
為坐標原點),求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】武漢有“九省通衢”之稱,也稱為“江城”,是國家歷史文化名城.其中著名的景點有黃鶴樓、戶部巷、東湖風景區等等.
(1)為了解“五·一”勞動節當日江城某旅游景點游客年齡的分布情況,從年齡在22歲到52歲的游客中隨機抽取了1000人,制成了如圖的頻率分布直方圖:
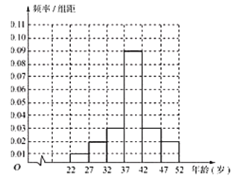
現從年齡在![]() 內的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機抽取4人,記4人中年齡在
內的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機抽取4人,記4人中年齡在![]() 內的人數為
內的人數為![]() ,求
,求![]() ;
;
(2)為了給游客提供更舒適的旅游體驗,該旅游景點游船中心計劃在2020年勞動節當日投入至少1艘至多3艘![]() 型游船供游客乘坐觀光.由2010到2019這10年間的數據資料顯示每年勞動節當日客流量
型游船供游客乘坐觀光.由2010到2019這10年間的數據資料顯示每年勞動節當日客流量![]() (單位:萬人)都大于1.將每年勞動節當日客流量數據分成3個區間整理得表:
(單位:萬人)都大于1.將每年勞動節當日客流量數據分成3個區間整理得表:
勞動節當日客流量 |
|
|
|
頻數(年) | 2 | 4 | 4 |
以這10年的數據資料記錄的3個區間客流量的頻率作為每年客流量在該區間段發生的概率,且每年勞動節當日客流量相互獨立.
該游船中心希望投入的![]() 型游船盡可能被充分利用,但每年勞動節當日
型游船盡可能被充分利用,但每年勞動節當日![]() 型游船最多使用量(單位:艘)要受當日客流量
型游船最多使用量(單位:艘)要受當日客流量![]() (單位:萬人)的影響,其關聯關系如下表:
(單位:萬人)的影響,其關聯關系如下表:
勞動節當日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在勞動節當日被投入且被使用,則游船中心當日可獲得利潤3萬元;若某艘
型游船在勞動節當日被投入且被使用,則游船中心當日可獲得利潤3萬元;若某艘![]() 型游船勞動節當日被投入卻不被使用,則游船中心當日虧損0.5萬元.記
型游船勞動節當日被投入卻不被使用,則游船中心當日虧損0.5萬元.記![]() (單位:萬元)表示該游船中心在勞動節當日獲得的總利潤,
(單位:萬元)表示該游船中心在勞動節當日獲得的總利潤,![]() 的數學期望越大游船中心在勞動節當日獲得的總利潤越大,問該游船中心在2020年勞動節當日應投入多少艘
的數學期望越大游船中心在勞動節當日獲得的總利潤越大,問該游船中心在2020年勞動節當日應投入多少艘![]() 型游船才能使其當日獲得的總利潤最大?
型游船才能使其當日獲得的總利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)對任意![]() ,
,![]() 都有恒成立,求實數a的取值范圍;
都有恒成立,求實數a的取值范圍;
(3)證明:對一切![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com