
【題目】已知定點![]() ,動點
,動點![]() 與
與![]() 、
、![]() 兩點連線的斜率之積為
兩點連線的斜率之積為![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知點![]() 是軌跡
是軌跡![]() 上的動點,點
上的動點,點![]() 在直線
在直線![]() 上,且滿足
上,且滿足![]() (其中
(其中![]() 為坐標原點),求
為坐標原點),求![]() 面積的最小值.
面積的最小值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)證明:![]() 為等比數列,求出
為等比數列,求出![]() 的通項公式;
的通項公式;
(2)若![]() ,求
,求![]() 的前n項和
的前n項和![]() ,并判斷是否存在正整數n使得
,并判斷是否存在正整數n使得![]() 成立?若存在求出所有n值;若不存在說明理由.
成立?若存在求出所有n值;若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除
給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,兩條平行線
,兩條平行線![]() 與
與![]() 間的距離為h,直線
間的距離為h,直線![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則該羨除的體積為
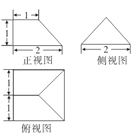
,則該羨除的體積為![]() 已知某羨除的三視圖如圖所示,則該羨除的體積為
已知某羨除的三視圖如圖所示,則該羨除的體積為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 和圓
和圓![]() 的普通方程;
的普通方程;
(2)已知直線![]() 上一點
上一點![]() ,若直線
,若直線![]() 與圓
與圓![]() 交于不同兩點
交于不同兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com