
【題目】已知函數![]() ,
,![]() .
.
(1)設函數![]() ,若
,若![]() ,求
,求![]() 的極值;
的極值;
(2)設函數![]() ,若
,若![]() 的圖象與
的圖象與![]() 的圖象有
的圖象有![]() ,
,![]() 兩個不同的交點,證明:
兩個不同的交點,證明:![]() .
.
【答案】(1)極大值為![]() ,極小值為
,極小值為![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)先求函數![]() 的導函數,再利用導數判斷函數的單調性,然后求極值即可;
的導函數,再利用導數判斷函數的單調性,然后求極值即可;
(2)函數![]() 的圖象與
的圖象與![]() 的圖象有兩個不同的交點,等價于關于
的圖象有兩個不同的交點,等價于關于![]() 的方程
的方程![]() ,即
,即![]() 有兩個不同的根,再構造函數
有兩個不同的根,再構造函數![]()
解:(1)因為![]() ,
,
所以![]() ,
,
![]() .
.
令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() ,
,![]() 上單調遞增;
上單調遞增;
令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調遞減.
上單調遞減.
故![]() 的極大值為
的極大值為![]() ,
,
故![]() 的極小值為
的極小值為![]() .
.
(2)證明:![]() ,
,
因為函數![]() 的圖象與
的圖象與![]() 的圖象有兩個不同的交點,
的圖象有兩個不同的交點,
所以關于![]() 的方程
的方程![]() ,即
,即![]() 有兩個不同的根.
有兩個不同的根.
由題知![]() ①,
①,![]() ②,
②,
①+②得![]() ③,
③,
②-①得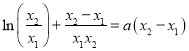 ④.
④.
由③,④得![]() ,
,
不妨設![]() ,記
,記![]() .
.
令![]() ,則
,則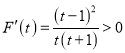 ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,
,
則![]() ,即
,即![]() ,
,
所以![]() .
.
因為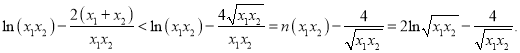
所以![]() ,
,
即![]() .
.
令![]() ,
,
則![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() .
.
兩邊同時取對數可得![]() ,
,
得證.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】德國著名數學家狄利克雷(Dirichlet,1805~1859)在數學領域成就顯著.19世紀,狄利克雷定義了一個“奇怪的函數” 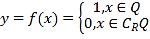 其中R為實數集,Q為有理數集.則關于函數
其中R為實數集,Q為有理數集.則關于函數![]() 有如下四個命題,正確的為( )
有如下四個命題,正確的為( )
A.函數![]() 是偶函數
是偶函數
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一個不為零的有理數T,![]() 對任意的
對任意的![]() 恒成立
恒成立
D.不存在三個點![]() ,
,![]() ,
,![]() ,使得
,使得![]() 為等腰直角三角形
為等腰直角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“回文數”是指從左到右與從右到左讀都一樣的正整數,如22,121,3553等.顯然2位“回文數”共9個:11,22,33,…,99.現從9個不同2位“回文數”中任取1個乘以4,其結果記為X;從9個不同2位“回文數”中任取2個相加,其結果記為Y.
(1)求X為“回文數”的概率;
(2)設隨機變量![]() 表示X,Y兩數中“回文數”的個數,求
表示X,Y兩數中“回文數”的個數,求![]() 的概率分布和數學期望
的概率分布和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王想在某市一住宅小區買套新房,據了解,該小區有若干棟互相平行的平頂樓房,每棟樓房有15層,每層樓高為3米,頂樓有1米高的隔熱層,兩樓之間相距60米.小王不想買最前面和最后面的樓房,但希望所買樓層全年每天正午都能曬到太陽.為此,小王查找了有關地理資料,獲得如下一些信息:①該市的緯度(地面一點所在球半徑與赤道平面所成的角)為北緯![]() ;②正午的太陽直射北回歸線(太陽光線與赤道平面所成的角為
;②正午的太陽直射北回歸線(太陽光線與赤道平面所成的角為![]() )時,物體的影子最短,直射南回歸線(太陽光線與赤道平面所成的角為
)時,物體的影子最短,直射南回歸線(太陽光線與赤道平面所成的角為![]() )時,物體的影子最長,那么小王買房的最低樓層應為( )
)時,物體的影子最長,那么小王買房的最低樓層應為( )
A.3B.4C.5D.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com