
 如圖,在多面體A1C1D1-ABCD中,平面A1C1D1∥平面ABCD,AA1∥DD1∥CC1,AA1⊥平面ABCD,四邊形為矩形,AD=1,DC=2,DD1=3.
如圖,在多面體A1C1D1-ABCD中,平面A1C1D1∥平面ABCD,AA1∥DD1∥CC1,AA1⊥平面ABCD,四邊形為矩形,AD=1,DC=2,DD1=3.分析 (1)以D為原點,建立空間直角坐標系D-xyz,利用向量法能求出實數λ的值.
(2)求出平面A1BC1的法向量,DH的最小值即為點D到平面A1BC1的距離,由此利用向量法能求出DH的最小值.
解答 解:(1)以D為原點,建立空間直角坐標系D-xyz,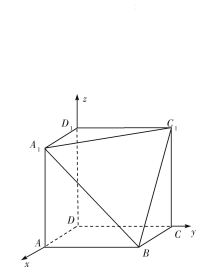
則D(0,0,0),A1(1,0,3),C1(0,2,3),B(1,2,0),
設E(x,y,z),則$\overrightarrow{{A}_{1}E}$=(x-1,y,z-3),$\overrightarrow{{A}_{1}{C}_{1}}$=(-1,2,0),
∵$\overrightarrow{{A}_{1}E}=λ\overrightarrow{{A}_{1}{C}_{1}}$,∴$\left\{\begin{array}{l}{x-1=-λ}\\{y=2λ}\\{z-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1-λ}\\{y=2λ}\\{z=3}\end{array}\right.$,
∴E(1-λ,2λ,3),
∴$\overrightarrow{DE}$=(1-λ,2λ,3),
∵DE⊥A1C1,∴$\overrightarrow{DE}•\overrightarrow{{A}_{1}{C}_{1}}$=(1-λ)×(-1)+2λ×2+3×0=0,
解得$λ=\frac{1}{5}$.
(2)$\overrightarrow{B{A}_{1}}$=(0,-2,3),$\overrightarrow{B{C}_{1}}$=(-1,0,3),
設平面A1BC1的法向量$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{B{A}_{1}}=-2y+3z=0}\\{\overrightarrow{n}•\overrightarrow{B{C}_{1}}=-x+3z=0}\end{array}\right.$,取z=2,得$\overrightarrow{n}$=(6,3,2),
DH的最小值即為點D到平面A1BC1的距離,
∵$\overrightarrow{D{A}_{1}}$=(1,0,3),∴DH的最小值d=$\frac{|\overrightarrow{D{A}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{12}{7}$.
點評 本題考查空間向量在立體幾何中的應用,考查運算求解能力、數形結合思想和函數與方程思想,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1] | B. | [3,+∞) | C. | (-∞,-3] | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
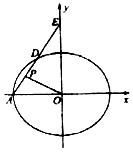 如圖,在平面平直角坐標系xOy中,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率e=$\frac{\sqrt{3}}{2}$,在頂點為A(-2,0),過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E.
如圖,在平面平直角坐標系xOy中,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率e=$\frac{\sqrt{3}}{2}$,在頂點為A(-2,0),過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x-2y+2=0 | B. | 2x+y-6=0 | C. | x+2y-2=0 | D. | 2x-y+6=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com