
分析 (1)確定出函數的定義域是解決本題的關鍵,利用導數作為工具,求出該函數的單調區間即可;
(2)方法一:利用函數思想進行方程根的判定問題是解決本題的關鍵.構造函數,研究構造函數的性質尤其是單調性,列出該方程有兩個相異的實根的不等式組,求出實數a的取值范圍.
方法二:先分離變量再構造函數,利用函數的導數為工具研究構造函數的單調性,根據題意列出關于實數a的不等式組進行求解.
解答 解:(1)函數f(x)的定義域為(1,+∞),
∵f′(x)=2[$\frac{1}{x-1}$-(x-1)]=-$\frac{2x(x-2)}{x-1}$,
∵x>1,則使f'(x)>0的x的取值范圍為(1,2),
令f′(x)<0,解得:x>2,
故函數f(x)的單調遞增區間為(1,2),遞減區間是(2,+∞);
(2)方法1:∵f(x)=2ln(x-1)-(x-1)2,
∴f(x)+x2-3x-a=0?x+a+1-2ln(x-1)=0.
令g(x)=x+a+1-2ln(x-1),
∵g'(x)=1-$\frac{2}{x-1}$=$\frac{x-3}{x-1}$,且x>1,
由g'(x)>0得x>3,g'(x)<0得1<x<3.
∴g(x)在區間[2,3]內單調遞減,在區間[3,4]內單調遞增,
故f(x)+x2-3x-a=0在區間[2,4]內恰有兩個相異實根
?$\left\{\begin{array}{l}{g(2)≥0}\\{g(3)<0}\\{g(4)≥0}\end{array}\right.$即 $\left\{\begin{array}{l}{a+3≥0}\\{a+4-2ln2<0}\\{a+5-2ln3≥0}\end{array}\right.$解得:2ln3-5≤a<2ln2-4.
綜上所述,a的取值范圍是[2ln3-5,2ln2-4).
方法2:∵f(x)=2ln(x-1)-(x-1)2,
∴f(x)+x2-3x-a=0?x+a+1-2ln(x-1)=0.
即a=2ln(x-1)-x-1,令h(x)=2ln(x-1)-x-1,
∵h'(x)=$\frac{2}{x-1}$-1=$\frac{3-x}{x-1}$,且x>1,
由h'(x)>0得1<x<3,h'(x)<0得x>3.
∴h(x)在區間[2,3]內單調遞增,在區間[3,4]內單調遞減.
∵h(2)=-3,h(3)=2ln2-4,h(4)=2ln3-5,又h(2)<h(4),
故f(x)+x2-3x-a=0在區間[2,4]內恰有兩個相異實根?h(4)≤a<h(3).
即2ln3-5≤a<2ln2-4.
綜上所述,a的取值范圍是[2ln3-5,2ln2-4).
點評 本題考查導數的工具作用,考查學生利用導數研究函數的單調性的知識.考查學生對方程、函數、不等式的綜合問題的轉化與化歸思想,將方程的根的問題轉化為函數的圖象交點問題,屬于綜合題型.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
 如圖,在多面體A1C1D1-ABCD中,平面A1C1D1∥平面ABCD,AA1∥DD1∥CC1,AA1⊥平面ABCD,四邊形為矩形,AD=1,DC=2,DD1=3.
如圖,在多面體A1C1D1-ABCD中,平面A1C1D1∥平面ABCD,AA1∥DD1∥CC1,AA1⊥平面ABCD,四邊形為矩形,AD=1,DC=2,DD1=3.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
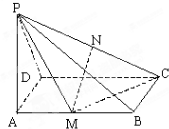 如圖所示,四棱錐P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥平面ABCD,M、N分別是AB、PC的中點.
如圖所示,四棱錐P-ABCD中,底面ABCD是矩形,PA=AD,PA⊥平面ABCD,M、N分別是AB、PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com