
【題目】如圖,四邊形![]() 是梯形,四邊形
是梯形,四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上的動點(diǎn).
上的動點(diǎn).
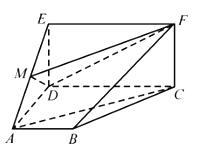
(1)試確定點(diǎn)![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)在(1)的條件下,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)![]() 是線段
是線段![]() 的中點(diǎn),理由見解析 (2)
的中點(diǎn),理由見解析 (2)![]()
【解析】
(1)當(dāng)![]() 是線段
是線段![]() 的中點(diǎn)時,
的中點(diǎn)時,![]() 平面
平面![]() .連結(jié)
.連結(jié)![]() ,交
,交![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,利用三角形中位線定理能夠證明
,利用三角形中位線定理能夠證明![]() 平面
平面![]() .
.
(2)法一:過點(diǎn)![]() 作平面
作平面![]() 與平面
與平面![]() 的交線
的交線![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,由已知條件推導(dǎo)出
,由已知條件推導(dǎo)出![]() 是平面
是平面![]() 與平面
與平面![]() 所成銳二面角的平面角,由此能求出所求二面角的余弦值.
所成銳二面角的平面角,由此能求出所求二面角的余弦值.
法二:分別以![]() ,
,![]() ,
,![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系![]() ,利用向量法能求出平面
,利用向量法能求出平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
解:(1)當(dāng)![]() 是線段
是線段![]() 的中點(diǎn)時,
的中點(diǎn)時,![]() 平面
平面![]() .
.

證明如下:
連結(jié)![]() ,交
,交![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,
,
由于![]() 分別是
分別是![]() ,
,![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() ,
,
由于![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

(2)方法1:過點(diǎn)![]() 作平面
作平面![]() 與平面
與平面![]() 的交線
的交線![]() ,
,
由于![]() 平面
平面![]() ,可知
,可知![]() ,
,
過點(diǎn)![]() 作
作![]() 于
于![]() ,
,
因?yàn)槠矫?/span>![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,則平面
,則平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
過![]() 作
作![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,則直線
,則直線![]() 平面
平面![]() ,
,
所以![]() ,
,
故![]() 是平面
是平面![]() 與平面
與平面![]() 所成銳二面角的平面角.
所成銳二面角的平面角.
設(shè)![]() ,則
,則![]() ,
,![]() ,
,
![]() ,則
,則 ,
,
所以![]() ,即所求二面角的余弦值為
,即所求二面角的余弦值為![]() .
.
方法2:

因?yàn)槠矫?/span>![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
可知![]() 兩兩垂直,分別以
兩兩垂直,分別以![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系![]() .
.
設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,設(shè)平面
,設(shè)平面![]() 的法向量
的法向量![]() ,
,
則 所以
所以![]()
令![]() ,得平面
,得平面![]() 的一個法向量
的一個法向量![]() ,
,
取平面![]() 的法向量
的法向量![]() ,
,
由 ,
,
故平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦距等于
的焦距等于![]() ,短軸與長軸的長度比等于
,短軸與長軸的長度比等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 在橢圓
在橢圓![]() 上,過
上,過![]() 作兩直線
作兩直線![]() ,分別交橢圓
,分別交橢圓![]() 于另外兩點(diǎn)
于另外兩點(diǎn)![]() ,當(dāng)
,當(dāng)![]() 的傾斜角互為補(bǔ)角時,求
的傾斜角互為補(bǔ)角時,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法:①若線性回歸方程為![]() ,則當(dāng)變量
,則當(dāng)變量![]() 增加一個單位時,
增加一個單位時,![]() 一定增加3個單位;②將一組數(shù)據(jù)中的每個數(shù)據(jù)都加上同一個常數(shù)后,方差不會改變;③線性回歸直線方程
一定增加3個單位;②將一組數(shù)據(jù)中的每個數(shù)據(jù)都加上同一個常數(shù)后,方差不會改變;③線性回歸直線方程![]() 必過點(diǎn)
必過點(diǎn)![]() ;④抽簽法屬于簡單隨機(jī)抽樣;其中錯誤的說法是( )
;④抽簽法屬于簡單隨機(jī)抽樣;其中錯誤的說法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年11月5日至10日,首屆中國國際進(jìn)口博覽會在國家會展中心(上海)舉行,吸引過來58個“一帶一路”沿線國家的超過1000多家企業(yè)參展,成為共建“一帶一路”的又一個重要支撐。某企業(yè)為了參加這次盛會,提升行業(yè)競爭力,加大了科技投入;該企業(yè)連續(xù)6年來得科技投入![]() (百萬元)與收益
(百萬元)與收益![]() (百萬元)的數(shù)據(jù)統(tǒng)計(jì)如下:
(百萬元)的數(shù)據(jù)統(tǒng)計(jì)如下:

根據(jù)散點(diǎn)圖的特點(diǎn),甲認(rèn)為樣本點(diǎn)分布在指數(shù)曲線![]() 的周圍,據(jù)此他對數(shù)據(jù)進(jìn)行了一些初步處理,如下表:
的周圍,據(jù)此他對數(shù)據(jù)進(jìn)行了一些初步處理,如下表:

其中![]() ,
,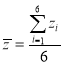 .
.
(1)(![]() )請根據(jù)表中數(shù)據(jù),建立
)請根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程(保留一位小數(shù));
的回歸方程(保留一位小數(shù));
(![]() )根據(jù)所建立回歸方程,若該企業(yè)想在下一年的收益達(dá)到2億,則科技投入的費(fèi)用至少要多少(其中
)根據(jù)所建立回歸方程,若該企業(yè)想在下一年的收益達(dá)到2億,則科技投入的費(fèi)用至少要多少(其中![]() )?
)?
(2)乙認(rèn)為樣本點(diǎn)分布在二次曲線![]() 的周圍,并計(jì)算得回歸方程為
的周圍,并計(jì)算得回歸方程為![]() ,以及該回歸模型的相關(guān)指數(shù)
,以及該回歸模型的相關(guān)指數(shù)![]() ,試比較甲乙兩位員工所建立的模型,誰的擬合效果更好.
,試比較甲乙兩位員工所建立的模型,誰的擬合效果更好.
附:對于一組數(shù)據(jù)![]() ,
,![]() ,……
,……![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計(jì)分別為
的斜率和截距的最小二乘估計(jì)分別為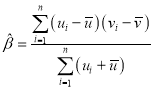 ,
,![]() ,相關(guān)指數(shù):
,相關(guān)指數(shù):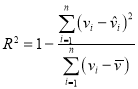 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高二理科8班共有50名學(xué)生參加學(xué)業(yè)水平模擬考試,成績(單位:分,滿分100分)大于或等于90分的為優(yōu)秀,其中語文成績近似服從正態(tài)分布![]() ,數(shù)學(xué)成績的頻率分布直方圖如圖.
,數(shù)學(xué)成績的頻率分布直方圖如圖.
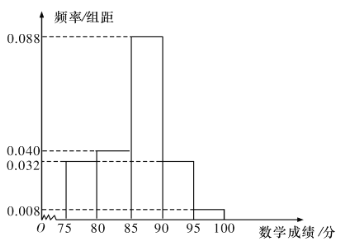
(I)這50名學(xué)生中本次考試語文、數(shù)學(xué)成績優(yōu)秀的大約各有多少人?
(Ⅱ)如果語文和數(shù)學(xué)兩科成績都優(yōu)秀的共有4人,從語文優(yōu)秀或數(shù)學(xué)優(yōu)秀的這些同學(xué)中隨機(jī)抽取3人,設(shè)3人中兩科都優(yōu)秀的有![]() 人,求
人,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(Ⅲ)根據(jù)(I)(Ⅱ)的數(shù)據(jù),是否有99%以上的把握認(rèn)為語文成績優(yōu)秀的同學(xué),數(shù)學(xué)成績也優(yōu)秀?
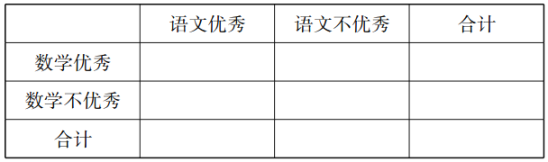
附:①若![]() ~
~![]() ,則
,則![]() ,
,![]() ;
;
②![]() ;
;
③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)y=f(x),x∈[1,+∞),數(shù)列{an}滿足![]() ,
,
①函數(shù)f(x)是增函數(shù);
②數(shù)列{an}是遞增數(shù)列.
寫出一個滿足①的函數(shù)f(x)的解析式______.
寫出一個滿足②但不滿足①的函數(shù)f(x)的解析式______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 是
是![]() 上任意一點(diǎn).
上任意一點(diǎn).
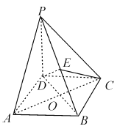
(1)求證![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點(diǎn),求
的中點(diǎn),求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 過點(diǎn)
過點(diǎn)![]() ,
,![]() 是拋物線
是拋物線![]() 上不同兩點(diǎn),且
上不同兩點(diǎn),且![]() (其中
(其中![]() 是坐標(biāo)原點(diǎn)),直線
是坐標(biāo)原點(diǎn)),直線![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,線段
,線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() .
.
(Ⅰ)求拋物線![]() 的準(zhǔn)線方程;
的準(zhǔn)線方程;
(Ⅱ)求證:直線![]() 與
與![]() 軸平行.
軸平行.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次![]() 公里的自行車個人賽中,25名參賽選手的成績(單位:分鐘)的莖葉圖如圖所示:
公里的自行車個人賽中,25名參賽選手的成績(單位:分鐘)的莖葉圖如圖所示:

(1)現(xiàn)將參賽選手按成績由好到差編為1~25號,再用系統(tǒng)抽樣方法從中選取5人,已知選手甲的成績?yōu)?5分鐘,若甲被選取,求被選取的其余4名選手的成績的平均數(shù);
(2)若從總體中選取一個樣本,使得該樣本的平均水平與總體相同,且樣本的方差不大于7,則稱選取的樣本具有集中代表性,試從總體(25名參賽選手的成績)選取一個具有集中代表性且樣本容量為5的樣本,并求該樣本的方差.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com