
分析 先求出直線方程的斜率,并表示出雙曲線方程的漸近線,再由雙曲線C:$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的一條漸近線與直線l:2x-y+1=0垂直可知兩直線的斜率之積等于-1,可求出a的值.
解答 解:直線l:2x-y+1=0的斜率等于2,雙曲線C:$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的漸近線可以表示為:y=±$\frac{x}{a}$
又因為雙曲線C:$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的一條漸近線與直線l:2x-y+1=0垂直,
∴2×(-$\frac{1}{a}$)=-1,∴a=2,
故答案為2
點評 本題主要考查雙曲線的基本性質--漸近線方程的表示,考查兩直線的位置關系.


 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:解答題
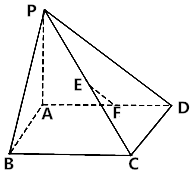 如圖,四棱錐P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,PA=AB=2.
如圖,四棱錐P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,PA=AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 轉速x(轉/秒-1) | 16 | 14 | 12 | 8 |
| 每小時生產有缺點的零件數y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$.A為橢圓上異于頂點的一點,點P滿足$\overrightarrow{OP}$=$2\overrightarrow{AO}$,
如圖,在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$.A為橢圓上異于頂點的一點,點P滿足$\overrightarrow{OP}$=$2\overrightarrow{AO}$,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{x-1}}}{2x+1}$ | B. | $-\frac{{\sqrt{x-1}}}{2x+1}$ | C. | $\frac{{\sqrt{x}}}{2x+3}$ | D. | $-\frac{{\sqrt{x}}}{2x+3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com