
分析 在100張卡片上分別寫上1至100這100個數字,從中任取一張共有100種取法,其中所得卡片上的數字為6的倍數的數是6,12,…,96,可得出滿足條件的數據的個數,再利用古典概型的概率計算公式即可得出.
解答 解:在100張卡片上分別寫上1至100這100個數字,從中任取一張共有100種取法,
其中所得卡片上的數字為6的倍數的數是:
6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96共16個,
∴所得卡片上的數字為6的倍數的數共有16個.
∴所得卡片上的數字為6的倍數的概率P=$\frac{16}{100}$=$\frac{4}{25}$,
故答案為:$\frac{4}{25}$.
點評 本題考查了古典概型的概率計算公式和等差數列的通項公式,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
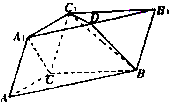 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D為A1B1的中點.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D為A1B1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
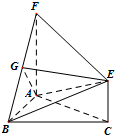 如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是線段BF上一點,AB=AF=BC.
如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是線段BF上一點,AB=AF=BC.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
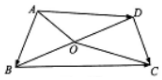 如圖,在平面四邊形ABCD中,O為BD的中點,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,則$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如圖,在平面四邊形ABCD中,O為BD的中點,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,則$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,3] | B. | [-2$\sqrt{2}$,3] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com