
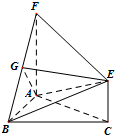
 如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是線段BF上一點(diǎn),AB=AF=BC.
如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是線段BF上一點(diǎn),AB=AF=BC.分析 (Ⅰ)由平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,可得AF⊥AC,則AF⊥平面ABC,得到平面ABF⊥平面ABC,過G作GD⊥AB,垂足為D,則GD⊥平面ABC,連接CD,可證得則四邊形GDCF為平行四邊形,從而得到GD=CE=$\frac{1}{2}AF$,則G為BF的中點(diǎn),得到$\frac{BG}{BF}$的值;
(Ⅱ)建立空間直角坐標(biāo)系,利用向量法即可求二面角E-BF-A的余弦值.
解答 解:(Ⅰ)∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,
AF⊥AC,∴AF⊥平面ABC,則平面ABF⊥平面ABC,
過G作GD⊥AB,垂足為D,則GD⊥平面ABC,連接CD,
由GD⊥平面ABC,AF⊥平面ABC,AF∥CE,可得GD∥CE,
又EG∥平面ABC,∴EG∥CD,則四邊形GDCF為平行四邊形,
∴GD=CE=$\frac{1}{2}AF$,
∴$\frac{BG}{BF}$=$\frac{1}{2}$;
(Ⅱ)由(Ⅰ)知AF⊥AB,AF⊥BC
∵BC⊥AB,∴BC⊥平面ABF.
如圖,以A為原點(diǎn),建立空間直角坐標(biāo)系A(chǔ)-xyz.
則F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1),
$\overrightarrow{BC}$=(0,2,0)是平面ABF的一個(gè)法向量.
設(shè)平面BEF的法向量$\overrightarrow{n}$=(x,y,z),則
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BE}=2y+z=0}\\{\overrightarrow{n}•\overrightarrow{BF}=-2x+2z=0}\end{array}\right.$,令y=1,則z=-2,x=-2,$\overrightarrow{n}$=(-2,1,-2),
∴cos<$\overrightarrow{n}$,$\overrightarrow{BC}$>=$\frac{\overrightarrow{n}•\overrightarrow{BC}}{|\overrightarrow{n}||\overrightarrow{BC}|}$=$\frac{1}{3}$,
∴二面角A-BF-E的正弦值為$\sqrt{1-(\frac{1}{3})^{2}}=\frac{2\sqrt{2}}{3}$.
點(diǎn)評 本題主要考查線面平行的判定以及空間二面角的計(jì)算,建立空間直角坐標(biāo)系,利用向量法是解決本題的關(guān)鍵,是中檔題.


 勵(lì)耘書業(yè)暑假銜接寧波出版社系列答案
勵(lì)耘書業(yè)暑假銜接寧波出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 命題“?x0∈R,x02-x0≤0”的否定為“?x∈R,x2-x>0” | |
| B. | 命題“在△ABC中,A>30°,則sinA>$\frac{1}{2}$”的逆否命題為真命題 | |
| C. | 設(shè){an}是公比為q的等比數(shù)列,則“q>1”是“{an}為遞增數(shù)列”的充分必要條件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$滿足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,則$\overrightarrow a$與$\overrightarrow b$共線 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2 | B. | -2017 | C. | 2017 | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $-\frac{11}{13}$ | B. | $-\frac{11}{12}$ | C. | $-\frac{7}{12}$ | D. | $-\frac{1}{13}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 如圖,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B與AB1交于點(diǎn)D,A1C與AC1交于點(diǎn)E.
如圖,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B與AB1交于點(diǎn)D,A1C與AC1交于點(diǎn)E.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,2) | D. | (1,+∞) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com