
【題目】在平面直角坐標系中,已知![]() ,若線段FP的中垂線l與拋物線C:
,若線段FP的中垂線l與拋物線C:![]() 總是相切.
總是相切.
(1)求拋物線C的方程;
(2)若過點Q(2,1)的直線l′交拋物線C于M,N兩點,過M,N分別作拋物線的切線![]() 相交于點A.
相交于點A.![]() 分別與y軸交于點B,C.
分別與y軸交于點B,C.
( i)證明:當![]() 變化時,
變化時,![]() 的外接圓過定點,并求出定點的坐標 ;
的外接圓過定點,并求出定點的坐標 ;
( ii)求![]() 的外接圓面積的最小值.
的外接圓面積的最小值.
【答案】(1)![]() ;(2)(i)證明見解析;(ii)
;(2)(i)證明見解析;(ii)![]() .
.
【解析】
(1)根據(jù)F(2,0),P(﹣2,t)得FP的中點為(0,![]() ),,討論t的值,當t≠0時,求出線段FP的中垂線l,代入拋物線方程y2=2px,
),,討論t的值,當t≠0時,求出線段FP的中垂線l,代入拋物線方程y2=2px,![]() 即可求解.
即可求解.
(2)設(shè)過點Q(2,1)的直線l′的方程為x﹣2=m(y﹣1),代入拋物線的方程y2=8x,
求出y1+y2=8m,y1y2=8m﹣16,對y2=8x兩邊求導得2yy′=8,即y′![]() ,求出
,求出![]() 處的切線方程,再求出
處的切線方程,再求出![]() ,設(shè)出外接圓的方程即可求出定點;由上一問可求出半徑,配方求半徑的最小值即可求解.
,設(shè)出外接圓的方程即可求出定點;由上一問可求出半徑,配方求半徑的最小值即可求解.
(1)F(2,0),P(﹣2,t),可得FP的中點為(0,![]() ),
),
當t=0時,FP的中點為原點,
當t≠0時,直線FP的斜率為![]() ,線段FP的中垂線l的斜率為
,線段FP的中垂線l的斜率為![]() ,
,
可得中垂線l的方程為y![]() x
x![]() ,代入拋物線方程y2=2px,
,代入拋物線方程y2=2px,
可得![]() x2+(4﹣2p)x
x2+(4﹣2p)x![]() 0,
0,
由直線和拋物線相切可得△=(4﹣2p)2﹣16=0,解得p=4,
則拋物線的方程為y2=8x;
(2)(i)證明:可設(shè)過點Q(2,1)的直線l′的方程為x﹣2=m(y﹣1),即x=my+2﹣m,
代入拋物線的方程y2=8x,可得y2﹣8my﹣16+8m=0,
設(shè)M(![]() ,y1),N(
,y1),N(![]() ,y2),則y1+y2=8m,y1y2=8m﹣16,
,y2),則y1+y2=8m,y1y2=8m﹣16,
由y2=8x,兩邊對x求導可得2yy′=8,即y′![]() ,
,
可得M處的切線方程為y﹣y1![]() (x
(x![]() ),化為y1y=4x
),化為y1y=4x![]() ,①
,①
同理可得N處的切線方程為y2y=4x![]() ,②
,②
由①②可得y![]() 4m,x
4m,x![]() m﹣2,即A(m﹣2,4m),
m﹣2,即A(m﹣2,4m),
又l1,l2分別與y軸交于點B(0,![]() ),C(0,
),C(0,![]() ),
),
設(shè)過A,B,C的外接圓的方程為x2+y2+Dx+Ey+F=0,(D2+E2﹣4F>0),
即有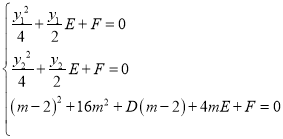
結(jié)合y1+y2=8m,y1y2=8m﹣16,可得D=﹣m﹣2,E=﹣4m,F=4m﹣8,
可得△ABC的外接圓方程為x2+y2﹣(m+2)x﹣4my+4m﹣8=0,
可得m(4﹣x﹣4y)+(x2+y2﹣2x﹣8)=0,
由![]() 可得
可得![]() 或
或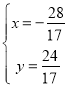 ,
,
則當l′變化時,△ABC的外接圓過定點(4,0)和(![]() ,
,![]() );
);

(ii)△ABC的外接圓的半徑
r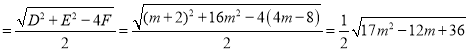 ,
,
可得當m![]() 時,r的最小值為
時,r的最小值為![]() ,
,
則△ABC的外接圓面積的最小值為![]() π.
π.


 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優(yōu)翼小幫手同步口算系列答案
優(yōu)翼小幫手同步口算系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
(1)若![]() ,求
,求![]() 的單調(diào)區(qū)間和極值點;
的單調(diào)區(qū)間和極值點;
(2)若![]() 在
在![]() 單調(diào)遞增,求實數(shù)
單調(diào)遞增,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的半焦距為
的半焦距為![]() ,圓
,圓![]() 與橢圓
與橢圓![]() 有且僅有兩個公共點,直線
有且僅有兩個公共點,直線![]() 與橢圓
與橢圓![]() 只有一個公共點.
只有一個公共點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知動直線![]() 過橢圓
過橢圓![]() 的左焦點
的左焦點![]() ,且與橢圓
,且與橢圓![]() 分別交于
分別交于![]() 兩點,試問:
兩點,試問:![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出該定值和點
為定值?若存在,求出該定值和點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,在矩形PABC中,AB=2BC=4,D為PC的中點,以AD為折痕將△PAD折起,折到如圖2的位置,使得PB=2![]() .
.

(1)求證:AP⊥平面PBD
(2)求平面PCD與平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若命題甲是命題乙的充分非必要條件,命題丙是命題乙的必要非充分條件,命題丁是命題丙的充要條件,則命題丁是命題甲的( )
A.充分不必要條件B.必要不充分條件C.充要條件D.既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ),
),![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)當![]() 時,求
時,求![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)若對任意的![]() ,
,![]() (
(![]() ),求
),求![]() 的最大值;
的最大值;
(3)若![]() 的極大值為
的極大值為![]() ,求不等式
,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的極值;
的極值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)函數(shù)![]() 的極值點為
的極值點為![]() ,當
,當![]() 變化時,點(
變化時,點(![]() ,
,![]() )構(gòu)成曲線M.證明:任意過原點的直線
)構(gòu)成曲線M.證明:任意過原點的直線![]() ,與曲線M均僅有一個公共點.
,與曲線M均僅有一個公共點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是定義在R上的偶函數(shù),對任意
是定義在R上的偶函數(shù),對任意![]() 都有
都有![]() ,當
,當![]() ,且
,且![]() 時,
時,![]() ,給出如下命題:
,給出如下命題:
①![]() ;
;
②直線![]() 是函數(shù)
是函數(shù)![]() 的圖象的一條對稱軸;
的圖象的一條對稱軸;
③函數(shù)![]() 在
在![]() 上為增函數(shù);
上為增函數(shù);
④函數(shù)![]() 在
在![]() 上有四個零點.
上有四個零點.
其中所有正確命題的序號為( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,O為BE中點,F為BC中點.將
,O為BE中點,F為BC中點.將![]() 沿BE折起到
沿BE折起到![]() 的位置,如圖2.
的位置,如圖2.
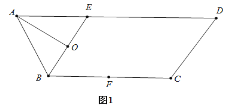
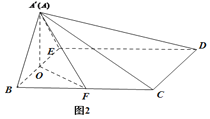
(1)證明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面BCDE,求點F到平面
平面BCDE,求點F到平面![]() 的距離.
的距離.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com