
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)設函數![]() 的極值點為
的極值點為![]() ,當
,當![]() 變化時,點(
變化時,點(![]() ,
,![]() )構成曲線M.證明:任意過原點的直線
)構成曲線M.證明:任意過原點的直線![]() ,與曲線M均僅有一個公共點.
,與曲線M均僅有一個公共點.
【答案】(1) ![]() 的極大值為
的極大值為![]() ,無極小值;(2)
,無極小值;(2) ![]() ;(3) 證明見解析.
;(3) 證明見解析.
【解析】
(1)對函數求導,求出單調區間,即可求出極值;
(2)![]() 恒成立,兩種解法:①分離參數,構造新函數,轉化為
恒成立,兩種解法:①分離參數,構造新函數,轉化為![]() 與新函數的最值關系;②轉化為
與新函數的最值關系;②轉化為![]() ,對
,對![]() 分類討論求出
分類討論求出![]() ,轉化為解關于
,轉化為解關于![]() 的不等式;
的不等式;
(3)先確定出點(![]() ,
,![]() )構成曲線M,直線
)構成曲線M,直線![]() 與曲線M均僅有一個公共點轉化為函數的零點,對
與曲線M均僅有一個公共點轉化為函數的零點,對![]() 分類討論,求出函數的單調區間,結合零點存在性定理,即可得證.
分類討論,求出函數的單調區間,結合零點存在性定理,即可得證.
(1)當![]() 時,
時,![]() ,
,
則![]()
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
所以當![]() 時,
時,![]() 的極大值為
的極大值為![]() ,無極小值;
,無極小值;
(2)(法一)∵![]() ,
,
∴由![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
令![]() 則
則![]() ,
,
令![]() ,則
,則![]() ,
,
∵![]() ,故
,故![]()
![]()
∴在![]() 在(0,+∞)單增,又
在(0,+∞)單增,又![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]()
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() 單減,
單減,![]() ),
),![]() 單增,
單增,
∴![]() 時,
時,![]() 取極小值即最小值
取極小值即最小值![]() ,
,
∴![]() ;
;
法二:![]()
由二次函數性質可知,存在![]() ,使得
,使得![]() ,
,
即![]() ,且當
,且當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
∴![]() ,
,
由題意可知,![]() ,
,
設![]() ,則
,則![]() ,即
,即![]() 單調遞增.
單調遞增.
∴![]() 的解集為(0,1],即
的解集為(0,1],即![]() ,
,
∴![]() ;
;
(3)由(2)可知![]() ,
,
則曲線M的方程為![]() ,
,
由題意可知.對任意![]() ,
,
證明:方程![]() 均有唯一解,
均有唯一解,
設![]() ,
,
則![]()
①當![]() 時,
時,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
∵![]() ,
,
![]()
所以存在![]() 滿足
滿足![]() 時,使得
時,使得![]() ,
,
又因為![]() 單調遞增.所以
單調遞增.所以![]() 為唯一解;
為唯一解;
②當![]() 且
且![]() ,即
,即![]() 時,
時,
![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
∵![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() ,
,
又∵![]() 單調遞增,所以
單調遞增,所以![]() 為唯一解;
為唯一解;
③當![]() 時,
時,![]() 有兩解
有兩解![]() ,不妨設
,不妨設![]() ,
,
因為![]() ,所以
,所以![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
由表可知,當![]() 時,
時,
![]() 的極大值為
的極大值為![]() ,
,
∵![]() ,所以
,所以![]() .
.
∴![]() ,
,
![]()
∴存在![]() ,使得
,使得![]() ,
,
又因為![]() 單調遞增,所以
單調遞增,所以![]() 為唯一解:
為唯一解:
綜上,原命題得證.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知![]() ,若線段FP的中垂線l與拋物線C:
,若線段FP的中垂線l與拋物線C:![]() 總是相切.
總是相切.
(1)求拋物線C的方程;
(2)若過點Q(2,1)的直線l′交拋物線C于M,N兩點,過M,N分別作拋物線的切線![]() 相交于點A.
相交于點A.![]() 分別與y軸交于點B,C.
分別與y軸交于點B,C.
( i)證明:當![]() 變化時,
變化時,![]() 的外接圓過定點,并求出定點的坐標 ;
的外接圓過定點,并求出定點的坐標 ;
( ii)求![]() 的外接圓面積的最小值.
的外接圓面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
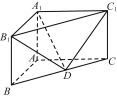
【題目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中點.
(1) 求直線DC1與平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點
的左焦點![]() ,離心率為
,離心率為![]() ,點P為橢圓E上任一點,且
,點P為橢圓E上任一點,且![]() 的最大值為
的最大值為![]() .
.
(1)求橢圓E的方程;
(2)若直線l過橢圓的左焦點![]() ,與橢圓交于A,B兩點,且
,與橢圓交于A,B兩點,且![]() 的面積為
的面積為![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的首項
的首項![]() ,且
,且![]() ,
,![]() .
.
(1)證明: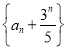 是等比數列;
是等比數列;
(2)若![]() ,
,![]() 中是否存在連續三項成等差數列?若存在,寫出這三項,若不存在,請說明理由;
中是否存在連續三項成等差數列?若存在,寫出這三項,若不存在,請說明理由;
(3)若![]() 是遞減數列,求
是遞減數列,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1、F2分別是雙曲線![]() 1(a>0,b>0)的左、右焦點,若雙曲線的右支上存在一點P,使得(
1(a>0,b>0)的左、右焦點,若雙曲線的右支上存在一點P,使得(![]() )
)![]() 0(O為坐標原點),且|PF1|
0(O為坐標原點),且|PF1|![]() |PF2|,則雙曲線的離心率的取值范圍是_____.
|PF2|,則雙曲線的離心率的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除
給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,兩條平行線
,兩條平行線![]() 與
與![]() 間的距離為h,直線
間的距離為h,直線![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則該羨除的體積為
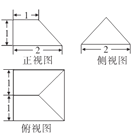
,則該羨除的體積為![]() 已知某羨除的三視圖如圖所示,則該羨除的體積為
已知某羨除的三視圖如圖所示,則該羨除的體積為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com