
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
分析 在同一坐標系內畫出函數$y={x}^{2}+1,y={2}^{x},y={x}^{2}+\frac{3}{2}$的圖象,可得$1≤{2}^{x}-{x}^{2}<\frac{3}{2}$,換元后分離參數a,求出函數值域得答案.
解答 解:在同一坐標系內畫出函數$y={x}^{2}+1,y={2}^{x},y={x}^{2}+\frac{3}{2}$的圖象如圖: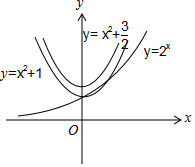
由圖可知,在x∈[0,1]上,${x}^{2}+1≤{2}^{x}<{x}^{2}+\frac{3}{2}$恒成立,
即$1≤{2}^{x}-{x}^{2}<\frac{3}{2}$,當且僅當x=0或x=1時等號成立.
∴1≤g(x)<$\frac{3}{2}$.設g(x)=t,則1$≤t<\frac{3}{2}$.
f[g(x)]≤0等價于f(t)≤0,
即cos($\frac{2π}{3}$t)+(a-1)sin($\frac{π}{3}$t)+a≤0,
∵1$≤t<\frac{3}{2}$,∴$\frac{π}{3}t$∈[$\frac{π}{3},\frac{π}{2}$),
再設sin$\frac{π}{3}t$=m,則$\frac{\sqrt{3}}{2}≤m<1$,
則原不等式可化為$1-2si{n}^{2}\frac{π}{3}t+(a-1)sin\frac{π}{3}t+a≤0$,
即1-2m2+(a-1)m+a≤0,
∴a$≤\frac{2{m}^{2}+m-1}{m+1}=2m-1$.
而$\sqrt{3}-1≤2m<1$,∴a$≤\sqrt{3}-1$.
故選:A.
點評 本題考查恒成立問題,考查三角函數的圖象和性質,體現了數形結合的解題思想方法,屬難題.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
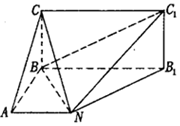 如圖,已知矩形BB1C1C所在平面與底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如圖,已知矩形BB1C1C所在平面與底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
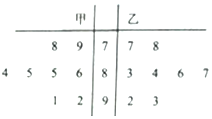 甲、乙兩名同學八次數學測試成績如莖葉圖所示,則甲同學成績的眾數與乙同學成績的中位數依次為( )
甲、乙兩名同學八次數學測試成績如莖葉圖所示,則甲同學成績的眾數與乙同學成績的中位數依次為( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com