
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 根據左加右減,寫出三角函數平移后的解析式,根據平移后圖象的對稱軸,把對稱軸代入使得函數式的值等于±1,寫出自變量的值,根據求最小值得到結果.
解答 解:∵把函數y=sin2x的圖象向右平移φ(φ>0)個單位,
∴平移后函數的解析式是y=sin(2x+2φ),
∵所得圖象關于直線 x=$\frac{π}{6}$對稱,
∴由正弦函數的圖象和性質可得:2×$\frac{π}{6}$+2φ=kπ+$\frac{π}{2}$(k∈Z),解得:φ=$\frac{1}{2}$kπ+$\frac{π}{12}$(k∈Z),
∵φ>0
∴當k=0時,φ的最小值是$\frac{π}{12}$.
故選:A.
點評 本題考查由三角函數圖象的平移求函數的解析式,本題解題的關鍵是先表示出函數的解析式,再根據題意來寫出結果,屬于基礎題.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
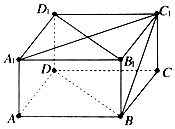 如圖,已知長方體ABCD-A1B1C1D1中,AB=BC=4,CC1=2,則直線BC1和平面DBB1D1所成角的正弦值等于( )
如圖,已知長方體ABCD-A1B1C1D1中,AB=BC=4,CC1=2,則直線BC1和平面DBB1D1所成角的正弦值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{x^2}$ | B. | $-\frac{1}{x^2}$ | C. | $\frac{1}{2x}$ | D. | $-\frac{1}{2x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
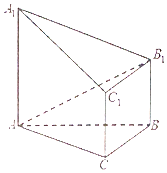 如圖,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.
如圖,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com