
【題目】已知函數f(x)=![]() ,若函數y=f(f(x))-a 恰有5個零點,則實數a的取值范圍為______.
,若函數y=f(f(x))-a 恰有5個零點,則實數a的取值范圍為______.
【答案】(0,ln2]∪{2}
【解析】
先作出函數f(x)的圖象,利用數形結合分類討論,即可確定實數a的取值范圍.
函數f(x)的圖象如圖,
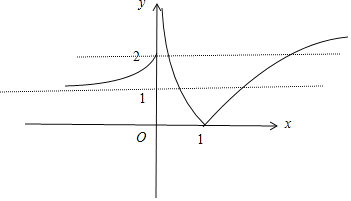
①當a=2時,則方程f(t)=2有3個根,且![]()
由圖象可知方程f(x)=t1有1根,方程f(x)=t2有2個根,方程f(x)=t3有2個根,共有5個根,故a=2符合題意;
②當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 有2個根,且
有2個根,且![]()
由圖象可知方程f(x)=t1有2根,方程f(x)=t2有2個根,共有4個根,故![]() 不符合題意;
不符合題意;
③當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 有2個根,且
有2個根,且![]()
由圖象可知方程f(x)=t1有2根,方程f(x)=t2有2個根,共有4個根,故![]() 不符合題意;
不符合題意;
④當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 有1個根,且
有1個根,且![]()
由圖象可知方程f(x)=1有2根,1故![]() 不符合題意;
不符合題意;
⑤當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 有3個根,且
有3個根,且![]() .
.
由圖象可知方程f(x)=t1有0根,方程f(x)=t2有2個根,方程f(x)=t3有2個根,共有4個根,故![]() 不符合題意;
不符合題意;
⑥當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 有2個根,且
有2個根,且![]() .
.
由圖象可知方程f(x)=t1有2根,方程f(x)=![]() 有3個根,共有5個根,
有3個根,共有5個根,
此時![]() ,故
,故![]() 符合題意;
符合題意;
⑦當![]() 時,則方程f(t)=
時,則方程f(t)=![]() 無根,不符合題意.
無根,不符合題意.
綜上:![]() ∪{2}.
∪{2}.
故答案為:(0,ln2]∪{2}.


科目:高中數學 來源: 題型:
【題目】若無窮數列{an}滿足:只要ap=aq(p,q∈N*),必有ap+1=aq+1 , 則稱{an}具有性質P.
(1)若{an}具有性質P,且a1=1,a2=2,a4=3,a5=2,a6+a7+a8=21,求a3;
(2)若無窮數列{bn}是等差數列,無窮數列{cn}是公比為正數的等比數列,b1=c5=1;b5=c1=81,an=bn+cn , 判斷{an}是否具有性質P,并說明理由;
(3)設{bn}是無窮數列,已知an+1=bn+sinan(n∈N*),求證:“對任意a1 , {an}都具有性質P”的充要條件為“{bn}是常數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法.如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例,若輸入n,x的值分別為3,2,則輸出v的值為( ) 
A.9
B.18
C.20
D.35
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,E、F、P、Q分別是BC、C1D1、AD1、BD的中點.

(1)求證:PQ∥平面DCC1D1;
(2)求證:AC⊥EF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以O為極點,x軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ=2(cos θ+sin θ).
(1)求C的直角坐標方程;
(2)直線l: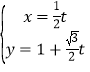 (t為參數)與曲線C交于A,B兩點,與y軸交于點E,求|EA|+|EB|.
(t為參數)與曲線C交于A,B兩點,與y軸交于點E,求|EA|+|EB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別是a,b,c,且 ![]() +
+ ![]() =
= ![]() .
.
(1)證明:sinAsinB=sinC;
(2)若b2+c2﹣a2= ![]() bc,求tanB.
bc,求tanB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ex+x﹣2,g(x)=lnx+x2﹣3,若實數a,b滿足f(a)=0,g(b)=0,則( )
A.0<g(a)<f(b)
B.f(b)<g(a)<0
C.f(b)<0<g(a)
D.g(a)<0<f(b)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com