
| A. | $8\sqrt{2}π$ | B. | $8(3-\sqrt{2})π$ | C. | $16(\sqrt{2}-1)π$ | D. | $16(2-\sqrt{2})π$ |
分析 設直線l與曲線的切點坐標為(x0,y0),求出函數的導數,可得切線的斜率和方程,聯立直線y=x求得A的坐標,與y軸的交點B的坐標,運用兩點距離公式和基本不等式可得AB的最小值,再由正弦定理可得外接圓的半徑,進而得到所求面積的最小值.
解答 解:設直線l與曲線的切點坐標為(x0,y0),
函數$y=\frac{{{x^2}+4}}{x}$的導數為$y'=\frac{{{x^2}-4}}{x^2}$.
則直線l方程為$y-\frac{x_0^2+4}{x_0}=\frac{x_0^2-4}{x_0^2}({x-{x_0}})$,即$y=\frac{x_0^2-4}{x_0^2}x+\frac{8}{x_0}$,
可求直線l與y=x的交點為A(2x0,2x0),與y軸的交點為$B({0,\frac{8}{x_0}})$,
在△OAB中,${|{AB}|^2}=4x_0^2+{({2{x_0}-\frac{8}{x_0}})^2}=8x_0^2+\frac{64}{x_0^2}-32≥32({\sqrt{2}-1})$,
當且僅當x02=2$\sqrt{2}$時取等號.
由正弦定理可得△OAB得外接圓半徑為$r=\frac{1}{2}\frac{{|{AB}|}}{{sin{{45}°}}}=\frac{{\sqrt{2}}}{2}|{AB}|$,
則△OAB外接圓面積$S=π{r^2}=\frac{1}{2}π{|{AB}|^2}≥16({\sqrt{2}-1})π$,
故選C.
點評 本題考查導數的運用:求切線方程,考查導數的幾何意義,同時考查正弦定理的運用,基本不等式的運用:求最值,以及化簡整理的運算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
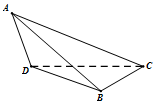 如圖,在三棱錐A-BCD中,△ABD為邊長等于$\sqrt{2}$正三角形,CD=CB=1.△ADC與△ABC是有公共斜邊AC的全等的直角三角形.
如圖,在三棱錐A-BCD中,△ABD為邊長等于$\sqrt{2}$正三角形,CD=CB=1.△ADC與△ABC是有公共斜邊AC的全等的直角三角形.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3個 | B. | 2個 | C. | 1個 | D. | 0個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(3)>f(2)>f(e) | D. | f(e)>f(3)>f(2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com