
【題目】在直角坐標系![]() 中,已知橢圓
中,已知橢圓![]()
![]()
![]() 的上頂點坐標為
的上頂點坐標為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓的標準方程;
(2)若橢圓上的點![]() 的橫坐標為
的橫坐標為![]() ,且位于第一象限,點
,且位于第一象限,點![]() 關于
關于![]() 軸的對稱點為點
軸的對稱點為點![]() ,
,![]() 是位于直線
是位于直線![]() 異側的橢圓上的動點.
異側的橢圓上的動點.
①若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
②若動點![]() 滿足
滿足![]() ,試探求直線
,試探求直線![]() 的斜率是否為定值?說明理由.
的斜率是否為定值?說明理由.
【答案】(1)![]() (2)①
(2)①![]() ②為定值,見解析
②為定值,見解析
【解析】
(1)直接根據橢圓的幾何性質求解;
(2)由(1)可得![]() 點坐標為
點坐標為![]() ,則
,則![]() ,
,
①設直線![]() 方程,聯立橢圓方程,設
方程,聯立橢圓方程,設![]() ,得韋達定理,表示出四邊形
,得韋達定理,表示出四邊形![]() 面積
面積![]() ,從而求出四邊形
,從而求出四邊形![]() 面積最大值為
面積最大值為![]() ;
;
②由題意可得直線![]() 斜率與直線
斜率與直線![]() 斜率互為相反數,設直線
斜率互為相反數,設直線![]() 的方程,聯立橢圓方程,設
的方程,聯立橢圓方程,設![]() ,得兩根之和,求得
,得兩根之和,求得![]() ,設
,設![]() ,同理可得
,同理可得![]() ,根據斜率計算公式得直線
,根據斜率計算公式得直線![]() 的斜率為定值.
的斜率為定值.
解:(1)由題意![]() ,可得
,可得![]() ,
,
則橢圓的標準方程為![]() ;
;
(2)由(1)可得![]() 點坐標為
點坐標為![]() ,則
,則![]() ,
,
①設直線![]() 方程為
方程為![]() ,聯立橢圓方程
,聯立橢圓方程![]() ,
,
化簡可得![]() ,
,
設![]() ,則
,則![]() ,
,
![]()
![]()
![]()
![]()
![]()
∴當![]() 時,四邊形
時,四邊形![]() 面積最大值為
面積最大值為![]() ;
;
②由題意,因為![]() ,則直線
,則直線![]() 斜率與直線
斜率與直線![]() 斜率互為相反數,
斜率互為相反數,
設直線![]() 的方程為
的方程為![]() ,聯立橢圓方程
,聯立橢圓方程![]() ,
,
化簡可得![]() ,設
,設![]() ,
,
則![]() ,又
,又![]() ,所以
,所以![]() ,
,
設![]() ,同理可得
,同理可得![]() ,
,
所以![]() ,
,
所以直線![]() 的斜率
的斜率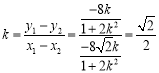 為定值.
為定值.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】某工廠生產![]() 、
、![]() 兩種零件,其質量測試按指標劃分,指標大于或等于
兩種零件,其質量測試按指標劃分,指標大于或等于![]() 的為正品,小于
的為正品,小于![]() 的為次品.現隨機抽取這兩種零件各100個進行檢測,檢測結果統計如下:
的為次品.現隨機抽取這兩種零件各100個進行檢測,檢測結果統計如下:
測試指標 |
|
|
|
|
|
| 8 | 12 | 40 | 30 | 10 |
| 9 | 16 | 40 | 28 | 7 |
(Ⅰ)試分別估計![]() 、
、![]() 兩種零件為正品的概率;
兩種零件為正品的概率;
(Ⅱ)生產1個零件![]() ,若是正品則盈利50元,若是次品則虧損10元;生產1個零件
,若是正品則盈利50元,若是次品則虧損10元;生產1個零件![]() ,若是正品則盈利60元,若是次品則虧損15元,在(Ⅰ)的條件下:
,若是正品則盈利60元,若是次品則虧損15元,在(Ⅰ)的條件下:
(i)設![]() 為生產1個零件
為生產1個零件![]() 和一個零件
和一個零件![]() 所得的總利潤,求
所得的總利潤,求![]() 的分布列和數學期望;
的分布列和數學期望;
(ii)求生產5個零件![]() 所得利潤不少于160元的概率.
所得利潤不少于160元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),若以該直角坐標系的原點
為參數),若以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() (其中
(其中![]() 為常數).
為常數).
(1)若曲線![]() 與曲線
與曲線![]() 有兩個不同的公共點,求
有兩個不同的公共點,求![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求曲線
時,求曲線![]() 上的點與曲線
上的點與曲線![]() 上點的最小距離.
上點的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大指出中國的電動汽車革命早已展開,通過以新能源汽車替代汽/柴油車,中國正在大力實施一項將重塑全球汽車行業的計劃.2018年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本2500萬元,每生產x(百輛),需另投入成本![]() 萬元,且
萬元,且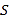 .由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
.由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2018年的利潤L(x)(萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額-成本)
(2)2018年產量為多少百輛時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2alnx.
(1)若函數f(x)的圖象在(2,f(2))處的切線斜率為1,求實數a的值;
(2)若函數![]() 在[1,2]上是減函數,求實數a的取值范圍.
在[1,2]上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設動直線![]() :
:![]() 分別與曲線
分別與曲線![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() ,求當
,求當![]() 為何值時,
為何值時,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com