
【題目】已知函數![]() ,若函數
,若函數![]() 在
在![]() 上無零點,則( )
上無零點,則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
因為f(x)<0在區間(0,![]() )上恒成立不可能,故要使函數f(x)在(0,
)上恒成立不可能,故要使函數f(x)在(0,![]() )上無零點,只要對任意的x∈(0,
)上無零點,只要對任意的x∈(0,![]() ),f(x)>0恒成立,然后利用參變量分離,利用導數研究不等式另一側的最值即可求出a的最小值.
),f(x)>0恒成立,然后利用參變量分離,利用導數研究不等式另一側的最值即可求出a的最小值.
解:因為f(x)<0在區間(0,![]() )上恒成立不可能,
)上恒成立不可能,
故要使函數f(x)在(0,![]() )上無零點,只要對任意的x∈(0,
)上無零點,只要對任意的x∈(0,![]() ),f(x)>0恒成立,
),f(x)>0恒成立,
即對x∈(0,![]() ),a>2
),a>2![]() 恒成立.
恒成立.
令l(x)=2![]() ,x∈(0,
,x∈(0,![]() ),
),
則l′(x)![]() ,
,
再令m(x)=2lnx![]() 2,x∈(0,
2,x∈(0,![]() ),
),
則m′(x)![]() 0,
0,
故m(x)在(0,![]() )上為減函數,于是m(x)>m(
)上為減函數,于是m(x)>m(![]() )=2﹣2ln2>0,
)=2﹣2ln2>0,
從而l′(x)>0,于是l(x)在(0,![]() )上為增函數,
)上為增函數,
所以l(x)<l(![]() )=2﹣4ln2,
)=2﹣4ln2,
故要使a>2![]() 恒成立,只要a∈[2﹣4ln2,+∞),
恒成立,只要a∈[2﹣4ln2,+∞),


科目:高中數學 來源: 題型:
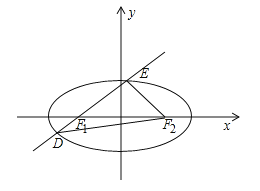
【題目】如圖,已知橢圓![]() ,
,![]() 分別為其左、右焦點,過
分別為其左、右焦點,過![]() 的直線與此橢圓相交于
的直線與此橢圓相交于![]() 兩點,且
兩點,且![]() 的周長為8,橢圓
的周長為8,橢圓![]() 的離心率為
的離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在平面直角坐標系![]() 中,已知點
中,已知點![]() 與點
與點![]() ,過
,過![]() 的動直線
的動直線![]() (不與
(不與![]() 軸平行)與橢圓相交于
軸平行)與橢圓相交于![]() 兩點,點
兩點,點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點.求證:
軸的對稱點.求證:
(i)![]() 三點共線.
三點共線.
(ii)![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】智能手機的出現,改變了我們的生活,同時也占用了我們大量的學習時間.某市教育機構從![]() 名手機使用者中隨機抽取
名手機使用者中隨機抽取![]() 名,得到每天使用手機時間(單位:分鐘)的頻率分布直方圖(如圖所示),其分組是:
名,得到每天使用手機時間(單位:分鐘)的頻率分布直方圖(如圖所示),其分組是: ![]() ,
,![]() .
.

(1)根據頻率分布直方圖,估計這![]() 名手機使用者中使用時間的中位數是多少分鐘? (精確到整數)
名手機使用者中使用時間的中位數是多少分鐘? (精確到整數)
(2)估計手機使用者平均每天使用手機多少分鐘? (同一組中的數據以這組數據所在區間中點的值作代表)
(3)在抽取的![]() 名手機使用者中在
名手機使用者中在![]() 和
和![]() 中按比例分別抽取
中按比例分別抽取![]() 人和
人和![]() 人組成研究小組,然后再從研究小組中選出
人組成研究小組,然后再從研究小組中選出![]() 名組長.求這
名組長.求這![]() 名組長分別選自
名組長分別選自![]() 和
和![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓周率是圓的周長與直徑的比值,一般用希臘字母![]() 表示,早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第七位的人,這比歐洲早了約1000年,在生活中,我們也可以通過設計下面的實驗來估計
表示,早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第七位的人,這比歐洲早了約1000年,在生活中,我們也可以通過設計下面的實驗來估計![]() 的值;從區間
的值;從區間![]() 內隨機抽取200個數,構成100個數對
內隨機抽取200個數,構成100個數對![]() ,其中滿足不等式
,其中滿足不等式![]() 的數對
的數對![]() 共有11個,則用隨機模擬的方法得到的
共有11個,則用隨機模擬的方法得到的![]() 的近似值為( )
的近似值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知橢圓
中,已知橢圓![]()
![]()
![]() 的上頂點坐標為
的上頂點坐標為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓的標準方程;
(2)若橢圓上的點![]() 的橫坐標為
的橫坐標為![]() ,且位于第一象限,點
,且位于第一象限,點![]() 關于
關于![]() 軸的對稱點為點
軸的對稱點為點![]() ,
,![]() 是位于直線
是位于直線![]() 異側的橢圓上的動點.
異側的橢圓上的動點.
①若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
②若動點![]() 滿足
滿足![]() ,試探求直線
,試探求直線![]() 的斜率是否為定值?說明理由.
的斜率是否為定值?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】吸煙有害健康,遠離煙草,珍惜生命。據統計一小時內吸煙5支誘發腦血管病的概率為0.02,一小時內吸煙10支誘發腦血管病的概率為0.16.已知某公司職員在某一小時內吸煙5支未誘發腦血管病,則他在這一小時內還能繼吸煙5支不誘發腦血管病的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不確定
D. 不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于復數![]() (
(![]()
![]() 為虛數單位),定義
為虛數單位),定義![]() ,給出下列命題:①對任何復數z,都有
,給出下列命題:①對任何復數z,都有![]() ,等號成立的充要條件是
,等號成立的充要條件是![]() ;②
;②![]() :③若
:③若![]() ,則
,則![]() :④對任何復數
:④對任何復數![]()
![]()
![]() ,不等式
,不等式![]() 恒成立,其中真命題的個數是( )
恒成立,其中真命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com