
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),若以該直角坐標系的原點
為參數),若以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() (其中
(其中![]() 為常數).
為常數).
(1)若曲線![]() 與曲線
與曲線![]() 有兩個不同的公共點,求
有兩個不同的公共點,求![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求曲線
時,求曲線![]() 上的點與曲線
上的點與曲線![]() 上點的最小距離.
上點的最小距離.
【答案】(Ⅰ)![]() 或
或![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
試題消去參數把曲線![]() 的參數方程化為普通方程,利用公式
的參數方程化為普通方程,利用公式![]() 把曲線
把曲線![]() 的極坐標方
的極坐標方
程化為直角坐標方程,利用數形結合的思想可以得出曲線![]() 有一個公共點時的
有一個公共點時的![]() 的范圍;(2)直線
的范圍;(2)直線
N:![]() ,設M上點為
,設M上點為![]() ,
,![]() ,則
,則![]()
![]() ,由此可求
,由此可求
得最小值.
試題解析:對于曲線M,消去參數,得普通方程為![]() ,曲線
,曲線![]() 是拋物線的一部分; 對于曲線N,化成直角坐標方程為
是拋物線的一部分; 對于曲線N,化成直角坐標方程為![]() ,曲線N是一條直線. (2分)
,曲線N是一條直線. (2分)
(1)若曲線M,N只有一個公共點,則有直線N過點![]() 時滿足要求,并且向左下方平行運動直到過點
時滿足要求,并且向左下方平行運動直到過點![]() 之前總是保持只有一個公共點,再接著向左下方平行運動直到相切之前總是有兩個公共點,所以
之前總是保持只有一個公共點,再接著向左下方平行運動直到相切之前總是有兩個公共點,所以![]() 滿足要求;相切時仍然只有一個公共點,由
滿足要求;相切時仍然只有一個公共點,由![]() ,得
,得![]()
![]() ,求得
,求得![]() .綜合可求得
.綜合可求得![]() 的取值范圍是:
的取值范圍是:![]() 或
或![]() . (6分)
. (6分)
(2)當![]() 時,直線N:
時,直線N:![]() ,設M上點為
,設M上點為![]() ,
,![]() ,則
,則
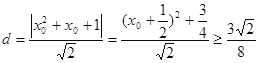 ,
,
當![]() 時取等號,滿足
時取等號,滿足![]() ,所以所求的最小距離為
,所以所求的最小距離為![]() . (10分)
. (10分)


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”是手機![]() 推出的多款健康運動軟件中的一款,大學生M的微信好友中有400位好友參與了“微信運動”.他隨機抽取了40位參與“微信運動”的微信好友(女20人,男20人)在某天的走路步數,經統計,其中女性好友走路的步數情況可分為五個類別:
推出的多款健康運動軟件中的一款,大學生M的微信好友中有400位好友參與了“微信運動”.他隨機抽取了40位參與“微信運動”的微信好友(女20人,男20人)在某天的走路步數,經統計,其中女性好友走路的步數情況可分為五個類別:![]() 、
、![]() 步,(說明:“
步,(說明:“![]() ”表示大于或等于0,小于2000,以下同理),
”表示大于或等于0,小于2000,以下同理),![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,且
步,且![]() 、
、![]() 、
、![]() 三種類別的人數比例為
三種類別的人數比例為![]() ,將統計結果繪制如圖所示的柱形圖;男性好友走路的步數數據繪制如圖所示的頻率分布直方圖.
,將統計結果繪制如圖所示的柱形圖;男性好友走路的步數數據繪制如圖所示的頻率分布直方圖.
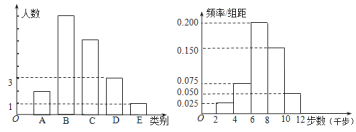
(Ⅰ)若以大學生![]() 抽取的微信好友在該天行走步數的頻率分布,作為參與“微信運動”的所有微信好友每天走路步數的概率分布,試估計大學生
抽取的微信好友在該天行走步數的頻率分布,作為參與“微信運動”的所有微信好友每天走路步數的概率分布,試估計大學生![]() 的參與“微信運動”的400位微信好友中,每天走路步數在
的參與“微信運動”的400位微信好友中,每天走路步數在![]() 的人數;
的人數;
(Ⅱ)若在大學生![]() 該天抽取的步數在
該天抽取的步數在![]() 的微信好友中,按男女比例分層抽取6人進行身體狀況調查,然后再從這6位微信好友中隨機抽取2人進行采訪,求其中至少有一位女性微信好友被采訪的概率.
的微信好友中,按男女比例分層抽取6人進行身體狀況調查,然后再從這6位微信好友中隨機抽取2人進行采訪,求其中至少有一位女性微信好友被采訪的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 點在底面
點在底面![]() 內的射影
內的射影![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() ,M在線段
,M在線段![]() 上,且
上,且![]() .
.
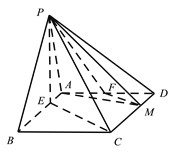
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)在線段AD上確定一點F,使得平面![]() 平面PAB,并求三棱錐
平面PAB,并求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知橢圓
中,已知橢圓![]()
![]()
![]() 的上頂點坐標為
的上頂點坐標為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓的標準方程;
(2)若橢圓上的點![]() 的橫坐標為
的橫坐標為![]() ,且位于第一象限,點
,且位于第一象限,點![]() 關于
關于![]() 軸的對稱點為點
軸的對稱點為點![]() ,
,![]() 是位于直線
是位于直線![]() 異側的橢圓上的動點.
異側的橢圓上的動點.
①若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
②若動點![]() 滿足
滿足![]() ,試探求直線
,試探求直線![]() 的斜率是否為定值?說明理由.
的斜率是否為定值?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年初,某市為了實現教育資源公平,辦人民滿意的教育,準備在今年8月份的小升初錄取中在某重點中學實行分數和搖號相結合的錄取辦法.該市教育管理部門為了了解市民對該招生辦法的贊同情況,隨機采訪了440名市民,將他們的意見和是否近三年家里有小升初學生的情況進行了統計,得到如下的2×2列聯表.
贊同錄取辦法人數 | 不贊同錄取辦法人數 | 合計 | |
近三年家里沒有小升初學生 | 180 | 40 | 220 |
近三年家里有小升初學生 | 140 | 80 | 220 |
合計 | 320 | 120 | 440 |
(1)根據上面的列聯表判斷,能否在犯錯誤的概率不超過0.001的前提下認為是否贊同小升初錄取辦法與近三年是否家里有小升初學生有關;
(2)從上述調查的不贊同小升初錄取辦法人員中根據近三年家里是否有小升初學生按分層抽樣抽出6人,再從這6人中隨機抽出3人進行電話回訪,求3人中恰有1人近三年家里沒有小升初學生的概率.
附:![]() ,其中
,其中![]() .
.
P( | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com