Question

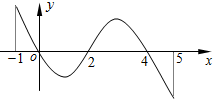
9．已知函數f（x）的定義域為[-1，5]，部分對應值如表：

x	-1	0	4	5
f（x）	1	2	2	1

f（x）的導函數y=f′（x）的圖象如圖所示：
下列關于函數f（x）的命題：
①函數y=f（x）是周期函數；
②函數f（x）在[0，2]是減函數；
③如果當x∈[-1，t]時，f（x）的最大值是2，那么t的最大值為4；
④當1＜a＜2時，函數y=f（x）-a有4個零點．
⑤函數y=f（x）-a的零點個數可能為0，1，2，3，4．
其中正確命題的個數是（　　）

• A． 3
• B． 2
• C． 1
• D． 0

Answer 1

分析 由導數圖象可知，函數的單調性，從而可得函數的極值，故可得①錯誤，②正確；因為在當x=0和x=4，函數取得極大值f（0）=2，f（4）=2，要使當x∈[-1，t]函數f（x）的最大值是4，當2≤t≤5，所以t的最大值為5，所以③不正確；由f（x）=a知，因為極小值f（2）未知，所以無法判斷函數y=f（x）-a有幾個零點，所以④不正確，根據函數的單調性和極值，做出函數的圖象如圖，即可求得結論．

解答 解：由導數圖象可知，當-1＜x＜0或2＜x＜4時，f'（x）＞0，函數單調遞增，
當0＜x＜2或4＜x＜5，f'（x）＜0，函數單調遞減，
當x=0和x=4，函數取得極大值f（0）=2，f（4）=2，當x=2時，函數取得極小值f（2），
所以①錯誤；②正確；
因為在當x=0和x=4，函數取得極大值f（0）=2，f（4）=2，
要使當x∈[-1，t]函數f（x）的最大值是4，
當2≤t≤5，所以t的最大值為5，所以③不正確；
由f（x）=a知，因為極小值f（2）未知，
所以無法判斷函數y=f（x）-a有幾個零點，所以④不正確，
根據函數的單調性和極值，做出函數的圖象如圖，（線段只代表單調性），

根據題意函數的極小值不確定，分f（2）＜1或1≤f（2）＜2兩種情況，
由圖象知，函數y=f（x）和y=a的交點個數有0，1，2，3，4等不同情形，所以⑤正確，
綜上正確的命題序號為②⑤．
故選：B．

點評 本題考查導數知識的運用，考查導函數與原函數圖象之間的關系，正確運用導函數圖象是關鍵．