
| A. | $\frac{33}{8}$ | B. | 6 | C. | 5 | D. | $\frac{69}{17}$ |
分析 根據等差數列的前n項和的性質,可得${S}_{15}=\frac{{15(a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$,${T}_{15}=\frac{15({b}_{1}+{b}_{15})}{2}$=$\frac{15×2{b}_{8}}{2}$,可得答案.
解答 解:根據等差數列的前n項和的性質,可得${S}_{15}=\frac{{15(a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$,${T}_{15}=\frac{15({b}_{1}+{b}_{15})}{2}$=$\frac{15×2{b}_{8}}{2}$,
那么$\frac{{S}_{15}}{{T}_{15}}$=$\frac{{a}_{8}}{{b}_{8}}$=$\frac{3×8+21}{8+1}$=5.
故選C
點評 本題考查了等差數列的前n項和的性質的運用.屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 老年人應作為重點調查對象,故抽取的老年人應超過40名 | |
| B. | 每個人被抽到的概率相同為$\frac{1}{10}$ | |
| C. | 應使用分層抽樣抽取樣本調查 | |
| D. | 抽出的樣本能在一定程度上反映總體的健康狀況 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | 12 | D. | -12 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
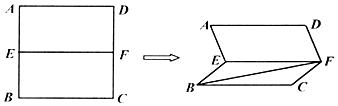 如圖,已知E,F分別是正方形ABCD的邊AB、CD的中點,現將正方形沿EF折成60°的二面角,則異面角直線AE與BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如圖,已知E,F分別是正方形ABCD的邊AB、CD的中點,現將正方形沿EF折成60°的二面角,則異面角直線AE與BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com