
分析 (1)由當n≥2時,Sn-1=2an-1-2,an=Sn-Sn-1,即可求得an=2an-1,則數列{an}是以2為首項,2為公比的等比數列;由$\frac{T_n}{{{T_{n+1}}}}=\frac{b_n}{{{b_{n+2}}}}$.采用“累乘法”即可求得當n≥2時,bn+1-bn-1=2,數列{bn}的奇數項,偶數項分別成立等差數列,b3=T2=b1+b2=3,b1+b3=2b2,數列{bn}是以b1=1為首項,1為公差的等差數列,即可求得數列{an}、{bn}的通項公式;
(2)設cn=$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$,作差比較大小,cn>cn+1>1,根據數列的單調性,即可求得存在n=2,使得b7=c2,b3=c3.
解答 解:(1)由Sn=2an-2,則當n≥2時,Sn-1=2an-1-2,
兩式相減得:an=2an-2an-1,則an=2an-1,
由S1=2a1-2,則a1=2,
∴數列{an}是以2為首項,2為公比的等比數列,則an=2n,
由$\frac{T_n}{{{T_{n+1}}}}=\frac{b_n}{{{b_{n+2}}}}$.
則$\frac{{T}_{1}}{{T}_{2}}$=$\frac{{b}_{1}}{{b}_{3}}$,$\frac{{T}_{2}}{{T}_{3}}$=$\frac{{b}_{2}}{{b}_{4}}$,$\frac{{T}_{3}}{{T}_{4}}$=$\frac{{b}_{3}}{{b}_{5}}$,…,$\frac{{T}_{n-1}}{{T}_{n}}$=$\frac{{b}_{n-1}}{{b}_{n+1}}$.$\frac{{T}_{n}}{{T}_{n+1}}$=$\frac{{b}_{n}}{{b}_{n+2}}$
以上各式相乘,$\frac{{T}_{1}}{{T}_{n+1}}$=$\frac{{b}_{1}{b}_{2}}{{b}_{n+1}{b}_{n+2}}$,則2Tn=bnbn+1,
當n≥2時,2Tn-1=bn-1bn,兩式相減得:2bn=bn(bn+1-bn-1),即bn+1-bn-1=2,
∴數列{bn}的奇數項,偶數項分別成等差數列,
由$\frac{{T}_{1}}{{T}_{2}}$=$\frac{{b}_{1}}{{b}_{3}}$,則b3=T2=b1+b2=3,b1+b3=2b2,
∴數列{bn}是以b1=1為首項,1為公差的等差數列,
∴數列{bn}的通項公式bn=n;
(2)當n=1時,$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$無意義,
設cn=$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$,(n≥2,n∈N*),
則cn+1-cn=$\frac{{2}^{n+1}+n+2}{{2}^{n+1}-(n+2)}$-$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$=$\frac{-n•{2}^{n+1}}{[{2}^{n+1}-(n+2)][{2}^{n}-(n+1)]}$<0,
即cn>cn+1>1,
顯然2n+n+1>2n-(n+1),則c2=7>c3=3>c4>…>1,
∴存在n=2,使得b7=c2,b3=c3,
下面證明不存在c2=2,否則,cn=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$=2,即2n=3(n+1),
此時右邊為3的倍數,而2n不可能是3的倍數,故該不等式成立,
綜上,滿足要求的bn為b3,b7.
點評 本題考查數列的綜合應用,考查等比數列及等差數列的通項公式及證明,考查數列單調性的判斷,考查轉化思想,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
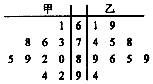 甲、乙兩位同學參加數學競賽培訓,培訓期間共參加了10次模擬考試,根據考試成績,得到如下圖所示的莖葉圖.規定模擬考試成績不低于81分為優秀等次.
甲、乙兩位同學參加數學競賽培訓,培訓期間共參加了10次模擬考試,根據考試成績,得到如下圖所示的莖葉圖.規定模擬考試成績不低于81分為優秀等次.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
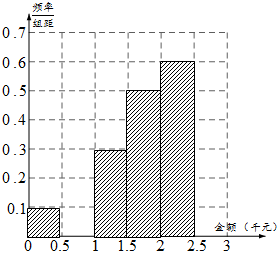 某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):
某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):| 網購金額 (單位千元) | 頻數 | 頻率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合計 | 60 | 1.00 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
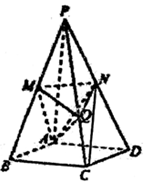 如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.
如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分別為PB,PD的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com