
分析 (1)利用誘導公式可求f(x)=1-2sin(2x-$\frac{π}{3}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,解得f(x)的單調遞增區間.
(2)由題意可得:2sin(2x-$\frac{π}{3}$)=1+b在[$\frac{π}{2}$,π]上有解,由2x-$\frac{π}{3}$∈[$\frac{2π}{3}$,$\frac{5π}{3}$],利用正弦函數的性質可得2sin(2x-$\frac{π}{3}$)=1+b∈[-2,$\sqrt{3}$],進而解得b的范圍.
(3)利用三角函數圖象變換規律可得g(x)=-2sin2x,①由題意可得$\frac{2π}{2ω}$≥2×2π,即可解得ω的范圍;
②由題意可得函數y=sin2ωx在區間(0,2π)上恰有三個取得最小值-1的點,利用正弦函數的圖象和性質可求$\frac{7T}{2}$≤2π<$\frac{9T}{2}$,根據三角函數周期公式可求ω的取值范圍.
解答 解:(1)∵f(x)=2sin($\frac{π}{3}$-2x)+1=1-2sin(2x-$\frac{π}{3}$).
∴令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,k∈Z,
∴f(x)的單調遞增區間為:[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
(2)∵若方程f(x)+b=0在[$\frac{π}{2}$,π]上有解,
∴1-2sin(2x-$\frac{π}{3}$)+b=0在[$\frac{π}{2}$,π]上有解,
可得:2sin(2x-$\frac{π}{3}$)=1+b,在[$\frac{π}{2}$,π]上有解,
∴由x∈[$\frac{π}{2}$,π],可得:2x-$\frac{π}{3}$∈[$\frac{2π}{3}$,$\frac{5π}{3}$],可得:2sin(2x-$\frac{π}{3}$)=1+b∈[-2,$\sqrt{3}$],
∴解得:b∈[-3,$\sqrt{3}$-1].
(3)將y=f(x)的圖象向左平移$\frac{π}{6}$個單位后,可得函數y=1-2sin[2(x+$\frac{π}{6}$)-$\frac{π}{3}$]=1-2sin2x,
再向下平移1個單位得到函數y=g(x)=-2sin2x,
①由題意可得:y=g(ωx)=-2sin2ωx的圖象在(-2π,0)上單調遞增,
∴$\frac{2π}{2ω}$≥2×2π,解得:ω≤$\frac{1}{4}$,
②∵-2sin2ωx=2,可得:sin2ωx=-1,
由題意,方程sin2ωx=-1在(0,2π)上至少存在三個根,
即函數y=sin2ωx在區間(0,2π)上恰有三個取得最小值-1的點,
∴$\frac{7T}{2}$≤2π<$\frac{9T}{2}$,求得:$\frac{4π}{9}$<T≤$\frac{4π}{7}$,即:$\frac{4π}{9}$<$\frac{2π}{2ω}$≤$\frac{4π}{7}$,解得:$\frac{7}{4}$≤ω<$\frac{9}{4}$.
即ω的取值范圍為:$\frac{7}{4}$≤ω<$\frac{9}{4}$.
點評 本題主要考查正弦函數的圖象特征和性質,正弦函數的最值,函數的零點,考查了轉化思想和數形結合思想的應用,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
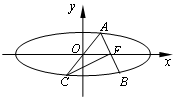 如圖,橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點為F,過F的直線交橢圓于A,B兩點,點C是點A關于原點O的對稱點,若CF⊥AB且CF=AB,則橢圓的離心率為$\sqrt{6}-\sqrt{3}$.
如圖,橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點為F,過F的直線交橢圓于A,B兩點,點C是點A關于原點O的對稱點,若CF⊥AB且CF=AB,則橢圓的離心率為$\sqrt{6}-\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{{2\sqrt{2}}}{9}$ | B. | $-\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{4}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ②④ | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com