
分析 (1)根據對數的定義可知負數和0沒有對數,列出關于x的不等式組,求出解集即可;要判斷函數的奇偶性即求出f(-x),判斷f(-x)與f(x)的關系可得;
(2)求出函數的導數,判斷導函數的符號,從而判斷函數的單調性即可;
(3)把f(x)的解析式代入到方程中利用對數的運算性質及對數的定義化簡得到g(x)=0,然后在(-1,1)上取幾個特殊值-$\frac{1}{2}$,0,-$\frac{1}{4}$,代入g(x)求出值判斷任意兩個乘積的正負即可知道之間是否有根.
解答 解:(1)要使函數有意義,則 $\left\{\begin{array}{l}{1-x>0}\\{1+x>0}\end{array}\right.$,
∴-1<x<1,故函數的定義域為(-1,1)
∵f(-x)=log2(1+x)-log2(1-x)=-f(x),
∴f(x)為奇函數.
(2)f(x)在(-1,1)遞減.
理由:f′(x)=$\frac{2}{(x+1)(x-1)ln2}$,
∵x+1>0,x-1<0,
故f′(x)<0,故f(x)在(-1,1)遞減;
(3)由題意知方程f(x)=x+1?log2(1-x)-log2(1+x)=x+1,
可化為(x+1)2x+1+x-1=0
設g(x)=(x+1)2x+1+x-1,x∈(-1,1)
則g(-$\frac{1}{2}$)=$\frac{1}{2}$×${2}^{\frac{1}{2}}$-$\frac{1}{2}$-1=$\frac{\sqrt{2}-3}{2}$<0,g(0)=2-1=1>0,
所以g(-$\frac{1}{2}$)g(0)<0,故方程在(-$\frac{1}{2}$,0)上必有根;
又因為g(-$\frac{1}{4}$)=$\frac{3}{4}$×${2}^{\frac{3}{4}}$-$\frac{1}{4}$-1=$\frac{\root{4}{648}-\root{4}{625}}{4}$>0,
所以g(-$\frac{1}{2}$)g(-$\frac{1}{4}$)<0,故方程在(-$\frac{1}{2}$,-$\frac{1}{4}$)上必有一根.
所以滿足題意的一個區間為(-$\frac{1}{2}$,-$\frac{1}{4}$).
點評 此題是一道綜合題,要求學生會求對數函數的定義域,會判斷函數的奇偶性,會判斷根的存在性和根的個數.在做第三問時注意會取特殊值.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{41}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
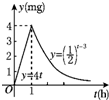 某醫藥研究所研發出一種新藥,成年人按規定的劑量服用后,據檢測,每毫升血液中的含藥量y(mg)與時間t(h)之間的關系如圖所示.據進一步測定,當每毫升血液中的含藥量不少于0.25mg時,治療疾病有效,則服藥一次,治療疾病有效的時間為( )
某醫藥研究所研發出一種新藥,成年人按規定的劑量服用后,據檢測,每毫升血液中的含藥量y(mg)與時間t(h)之間的關系如圖所示.據進一步測定,當每毫升血液中的含藥量不少于0.25mg時,治療疾病有效,則服藥一次,治療疾病有效的時間為( )| A. | 4 h | B. | 4$\frac{7}{8}$ h | C. | 4$\frac{15}{16}$ h | D. | 5 h |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com