
分析 (Ⅰ)先對函數f(x)進行求導,根據 f'(1)=0,f'(3)=24確定函數的解析式,然后令f'(x)<0求單調遞減區間;
(Ⅱ)把a=1代入函數f(x)后對函數進行求導,由題意可得f′(x)=3x2+b≤0在[-1,1]上恒成立,分離參數b得答案.
解答 解:(Ⅰ)已知函數f(x)=ax3+bx(x∈R),∴f′(x)=3ax2+b,
又函數f(x)圖象在點x=3處的切線與直線24x-y+1=0平行,
且函數f(x)在x=1處取得極值,∴f′(3)=27a+b=24,
且f′(1)=3a+b=0,解得a=1,b=-3,
∴f(x)=x3-3x.
令f′(x)=3x2-3≤0,得-1≤x≤1,
∴函數的單調遞減區間為[-1,1]
(Ⅱ)當a=1時,f(x)=x3+bx(x∈R),又函數f(x)在[-1,1]上是減函數,
∴f′(x)=3x2+b≤0在[-1,1]上恒成立.
即b≤-3x2在[-1,1]上恒成立,∴b≤-3.
點評 本題考查利用導數研究過曲線上某點處的切線方程,考查了利用導數研究函數的單調性,屬中檔題.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-8] | B. | (-∞,-8) | C. | (-∞,-6] | D. | (-∞,-6) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
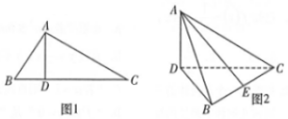 如圖1,在Rt△ABC中,∠ABC=60°,AD是斜邊BC上的高,沿AD將△ABC折成60°的二面角B-AD-C,如圖2.
如圖1,在Rt△ABC中,∠ABC=60°,AD是斜邊BC上的高,沿AD將△ABC折成60°的二面角B-AD-C,如圖2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com