
分析 橢圓的離心率是e=$\frac{c}{a}$,則a=2b,則橢圓的方程可化為:x2+4y2=4b2.設M(m,n),直線AB的方程為:y=kx,可設:A(x0,kx0),B(-x0,-kx0).代入橢圓方程和利用斜率計算公式即可得出.
解答 解:∵橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率是e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,a=2b,
于是橢圓的方程可化為:x2+4y2=4b2.
設M(m,n),直線AB的方程為:y=kx,可設:A(x0,kx0),B(-x0,-kx0).
則m2+4n2=4b2,x02+4k2x02=4b2.
m2-x02=4k2x02-4n2,
∴k1•k2=$\frac{k{x}_{0}-n}{{x}_{0}-m}$×$\frac{-k{x}_{0}-n}{-{x}_{0}-m}$=$\frac{{n}^{2}-{k}^{2}{x}_{0}^{2}}{{m}^{2}-{x}_{0}^{2}}$=$\frac{{n}^{2}-{k}^{2}{x}_{0}^{2}}{4{k}^{2}{x}_{0}^{2}-4{n}^{2}}$=-$\frac{1}{4}$.
k1•k2=-$\frac{1}{4}$.
故答案為:-$\frac{1}{4}$.
點評 本題考查了橢圓的標準方程及其性質、斜率計算公式等基礎知識與基本技能方法,屬于中檔題.


 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:選擇題
| A. | [-3e-4,1) | B. | [-3e-4,1)∪{-e-2} | C. | [0,1)∪{-e-2} | D. | [0,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{3-2\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,e) | B. | (-∞,e) | C. | {e} | D. | (-∞,0)∪{e} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
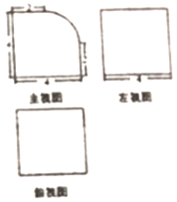
| A. | 64-4π | B. | 64+6π | C. | 48+4π | D. | 64-6π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com