日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

7．已知二項(xiàng)式${（\root{3}{x^2}+\frac{1}{x}）^n}$的展開(kāi)式中含有x2的項(xiàng)是第3項(xiàng)，則n=8．

分析 首先寫(xiě)出展開(kāi)式的通項(xiàng)，由題意得到關(guān)于n 的等式解之．

解答 解：二項(xiàng)式${（\root{3}{x^2}+\frac{1}{x}）^n}$的展開(kāi)式中通項(xiàng)為${T}_{r+1}={C}_{n}^{r}（\root{3}{{x}^{2}}）^{n-r}（\frac{1}{x}）^{r}$=${C}_{n}^{r}{x}^{\frac{2n-5r}{3}}$，
因?yàn)檎归_(kāi)式中含有x2的項(xiàng)是第3項(xiàng)，所以r=2時(shí)2n-5r=6，解得n=8；
故答案為：8．

點(diǎn)評(píng) 本題考查了二項(xiàng)式定理的運(yùn)用；熟練掌握展開(kāi)式的通項(xiàng)是解答的關(guān)鍵．

練習(xí)冊(cè)系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

17．已知函數(shù)f（x）=cos2$\frac{x}{2}$-sin$\frac{x}{2}$cos$\frac{x}{2}$-$\frac{1}{2}$．
（1）求函數(shù)f（x）的最小正周期和值域 
（2）求函數(shù)單調(diào)遞減區(qū)間
（3）若f（α）=$\frac{{3\sqrt{2}}}{10}$，求sin 2α的值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：選擇題

18．已知△ABC中，AC=$\sqrt{2}，BC=\sqrt{6}$，∠ACB=$\frac{π}{6}$，若線(xiàn)段BA的延長(zhǎng)線(xiàn)上存在點(diǎn)D，使∠BDC=$\frac{π}{4}$，則CD=（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．3D．$2\sqrt{3}$

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：選擇題

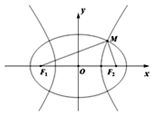15．已知橢圓C1：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）與雙曲線(xiàn)C2：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦點(diǎn)F1，F(xiàn)2，設(shè)M為C1與C2在第一象限內(nèi)的交點(diǎn)，|F1F2|=2c．則（　　）
A．m2+n2=2c2，且∠F1MF2＞$\frac{π}{2}$B．m2+n2=2c2，且∠F1MF2=$\frac{π}{2}$
C．m2+n2=4c2，且∠F1MF2＞$\frac{π}{2}$D．m2+n2=4c2，且∠F1MF2=$\frac{π}{2}$

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

2．已知函數(shù)f（x）=|x-2|-|x+1|．
（Ⅰ）解不等式f（x）+x＞0；
（Ⅱ）若關(guān)于x的不等式f（x）≤a2-2a在R上的解集為R，求實(shí)數(shù)a的取值范圍．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：選擇題

12．已知{an}是公差為2的等差數(shù)列，若a1，a3，a4成等比數(shù)列，則a2=（　　）
A．-4B．-8C．-10D．-6

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：選擇題

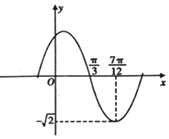19．函數(shù)f（x）=Asin（ωx+φ），（A，ω，φ是常數(shù)，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分圖象如圖所示，則y=f（x）在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上的取值范圍是（　　）
A．[-$\frac{\sqrt{2}}{2}$，$\sqrt{2}$]B．[$\frac{\sqrt{2}}{2}$，$\sqrt{2}$]C．[-$\frac{\sqrt{6}}{2}$，$\sqrt{2}$]D．[$\frac{\sqrt{6}}{2}$，$\sqrt{2}$]

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

16．設(shè)函數(shù)f（x）=|x-$\frac{4}{m}$|+|x+m|，（m＞0）
（I）證明：f（x）≥4
（II）若f（1）＞5，求m的取值范圍．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

1．極坐標(biāo)系中橢圓C的方程為ρ2=$\frac{2}{co{s}^{2}θ+2si{n}^{2}θ}$，以極點(diǎn)為原點(diǎn)，極軸為x軸非負(fù)半軸，建立平面直角坐標(biāo)系，且兩坐標(biāo)系取相同的單位長(zhǎng)度．
（1）若橢圓上任一點(diǎn)坐標(biāo)為P（x，y），求${x^2}+\sqrt{2}xy$的取值范圍；
（2）若橢圓的兩條弦AB，CD交于點(diǎn)Q，且直線(xiàn)AB與CD的傾斜角互補(bǔ)，求證：|QA|•|QB|=|QC|•|QD|．

查看答案和解析>>

同步練習(xí)冊(cè)答案
主站蜘蛛池模板： 久久er99热精品一区二区 | 国产精品成人一区二区 | 国产区免费视频 | 国产视频久久精品 | 国产精品国色综合久久 | 三级av网站 | 亚洲 欧美 综合 | 电影k8一区二区三区久久 | 91精品国产自产精品男人的天堂 | 一区二区免费在线观看 | 香蕉视频91 | 成人性大片免费观看网站 | 成人亚洲视频 | 91欧美在线 | 欧美精品网站 | 色婷婷中文字幕 | 中文字幕一区二区三区在线视频 | 久久精品这里热有精品 | 娇小12—13毛片 | 4hu在线 | 欧美成人久久久免费播放 | 91精品国产色综合久久不卡98口 | 日韩福利在线观看 | 国产精品自拍av | 欧美激情综合五月色丁香小说 | 丁香五月网久久综合 | 国产在线第一页 | 国产成人精品久久二区二区91 | 亚洲精品乱码 | 国产精品久久在线观看 | 国产永久免费观看 | 欧美日韩精品一区二区 | 精品国产乱码久久久久久久软件 | 久久久精品一区二区 | 亚洲成人免费视频 | 午夜激情影院在线观看 | 毛片网站大全 | 色婷婷一区二区三区四区 | 国产不卡福利片 | 成人精品一区二区三区电影黑人 | 日韩成人免费 |