
分析 (1)根據橢圓的性質,及橢圓的通徑,即可求得a和b的值;
(2)分別求得直線A1M,A2M的方程,代入橢圓方程,即可求得P,Q坐標,根據直線的斜率公式,即可求得直線PQ是否恒過定點.
解答 解:(1)由題意的焦點在x軸上,設橢圓方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,則a2=4b2,由題意的通徑$\frac{2{b}^{2}}{a}$=1,
解得:a=2,b=1,
∴橢圓的標準方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)由(1)知橢圓C的標準方程為$\frac{{x}^{2}}{4}+{y}^{2}=1$,則A1(-2,0),A2(2,0),
M(-4,m)(m∈R,且m≠0)P(x1,y1).Q(x2,y2)
${k}_{{A}_{1}M}$=$\frac{m-0}{-4+2}$=-$\frac{m}{2}$,${k}_{{A}_{2}M}$=$\frac{m-0}{-4-2}$=-$\frac{m}{6}$,
∴A1M:y=-$\frac{m}{2}$(x+2),A2M:y=-$\frac{m}{6}$(x-2),
$\left\{\begin{array}{l}{y=-\frac{m}{2}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:(m2+1)x2+4m2x+4m2-4=0,
-2x1=$\frac{4{m}^{2}-4}{{m}^{2}+1}$,x1=-$\frac{2{m}^{2}-2}{{m}^{2}+1}$,y1=-$\frac{m}{2}$(x1+2)=-$\frac{2m}{{m}^{2}+1}$,
P(-$\frac{2{m}^{2}-2}{{m}^{2}+1}$,-$\frac{2m}{{m}^{2}+1}$),
由$\left\{\begin{array}{l}{y=-\frac{m}{6}(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y得:(m2+9)x2-4m2x+4m2-36=0,
∴2x2=$\frac{4{m}^{2}-36}{{m}^{2}+9}$,∴x2=$\frac{2{m}^{2}-18}{{m}^{2}+9}$,y2=-$\frac{m}{6}$(x2-2)=$\frac{6m}{{m}^{2}+9}$,
Q($\frac{2{m}^{2}-18}{{m}^{2}+9}$,$\frac{6m}{{m}^{2}+9}$).
則kPQ=kPQ=$\frac{2m}{3-{m}^{2}}$(m≠±$\sqrt{3}$),y+$\frac{2m}{{m}^{2}+1}$=$\frac{2m}{3-{m}^{2}}$(x+$\frac{2{m}^{2}-2}{{m}^{2}+1}$),
y=$\frac{2m}{3-{m}^{2}}$x-$\frac{2m}{{m}^{2}+1}$=$\frac{2m}{3-{m}^{2}}$(x+1),
∴直線PQ恒過定點(-1,0),
當m=$\sqrt{3}$時,P(-1,-$\frac{\sqrt{3}}{2}$),Q(-1,$\frac{\sqrt{3}}{2}$),當m=-$\sqrt{3}$時,P(-1,$\frac{\sqrt{3}}{2}$),Q(-1,-$\frac{\sqrt{3}}{2}$),
直線PQ恒過定點(-1,0),
∴綜上可知:直線PQ恒過定點(-1,0),
點評 通過直線與圓錐曲線的位置關系處理,考查學生的運算能力.通過方程與幾何問題的綜合,考查學生分析轉化問題的能力,探究研究問題的能力,并體現了合理消元,設而不解的代數變形的思想,屬于中檔題.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:選擇題
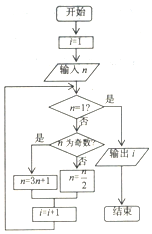 20世紀70年代,流行一種游戲---角谷猜想,規則如下:任意寫出一個自然數n,按照以下的規律進行變換:如果n是個奇數,則下一步變成3n+1;如果n是個偶數,則下一步變成$\frac{n}{2}$,這種游戲的魅力在于無論你寫出一個多么龐大的數字,最后必然會落在谷底,更準確的說是落入底部的4-2-1循環,而永遠也跳不出這個圈子,下列程序框圖就是根據這個游戲而設計的,如果輸出的i值為6,則輸入的n值為( )
20世紀70年代,流行一種游戲---角谷猜想,規則如下:任意寫出一個自然數n,按照以下的規律進行變換:如果n是個奇數,則下一步變成3n+1;如果n是個偶數,則下一步變成$\frac{n}{2}$,這種游戲的魅力在于無論你寫出一個多么龐大的數字,最后必然會落在谷底,更準確的說是落入底部的4-2-1循環,而永遠也跳不出這個圈子,下列程序框圖就是根據這個游戲而設計的,如果輸出的i值為6,則輸入的n值為( )| A. | 5 | B. | 16 | C. | 5或32 | D. | 4或5或32 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
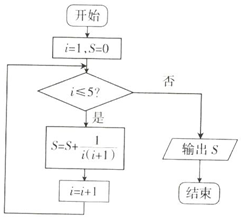
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
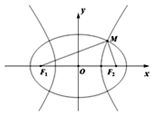 已知橢圓C1:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1(m>p>0)與雙曲線C2:$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1(n>0)有公共的焦點F1,F2,設M為C1與C2在第一象限內的交點,|F1F2|=2c.則( )
已知橢圓C1:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1(m>p>0)與雙曲線C2:$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1(n>0)有公共的焦點F1,F2,設M為C1與C2在第一象限內的交點,|F1F2|=2c.則( )| A. | m2+n2=2c2,且∠F1MF2>$\frac{π}{2}$ | B. | m2+n2=2c2,且∠F1MF2=$\frac{π}{2}$ | ||
| C. | m2+n2=4c2,且∠F1MF2>$\frac{π}{2}$ | D. | m2+n2=4c2,且∠F1MF2=$\frac{π}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com