Question

20．已知平面區(qū)域D={（x，y）|$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$}，Z=$\frac{y}{x+2}$．若命題“?（x，y）∈D，Z≥m”為真命題，則實(shí)數(shù)m的最大值為（　　）

• A． $\frac{22}{15}$
• B． $\frac{2}{7}$
• C． $\frac{1}{3}$
• D． $\frac{1}{4}$

Answer 1

分析 由已知，即求Z的最小值，利用數(shù)形結(jié)合的思想求Z的最大值即可．

解答 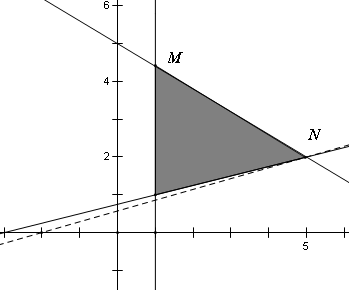解：由題意命題“?（x，y）∈D，Z≥m”為真命題即求Z的最小值，平面區(qū)域如圖：Z=$\frac{y}{x+2}$表示區(qū)域內(nèi)的點(diǎn)與定點(diǎn)（-2，0）連接直線(xiàn)的斜率，所以與n鄰居的直線(xiàn)斜率最小，由$\left\{\begin{array}{l}{x-4y+3=0}\\{3x+5y-25=0}\end{array}\right.$得到N（5，2），所以最小值為$\frac{2}{5+2}=\frac{2}{7}$，
所以實(shí)數(shù)m≤$\frac{2}{7}$，所以M的最大值為$\frac{2}{7}$；
故選：B．

點(diǎn)評(píng) 本題考查了簡(jiǎn)單線(xiàn)性規(guī)劃問(wèn)題以及全稱(chēng)命題求參數(shù)范圍；關(guān)鍵是正確求出Z的最小值，利用了數(shù)形結(jié)合的思想．