
分析 若函數f(x)有2個不同的零點,則$\frac{|x|}{x+2}$-kx2=0 ①有2個不同的實數根.再分(1)當x=0時、(2)x≠0時2種情況,分別求出方程的根,綜合可得方程①有2個不相等的實數根的條件.
解答 解:若函數f(x)=$\frac{\left|x\right|}{x+2}$-kx2(k∈R)有兩個零點,
則$\frac{\left|x\right|}{x+2}$-kx2=0 ①有兩個不同的實數根.
(1)當x=0時,不論k取何值,方程①恒成立,即x=0恒為方程①的一個實數解.
(2)故只需x≠0,函數f(x)=$\frac{\left|x\right|}{x+2}$-kx2(k∈R)有1個零點
?$\frac{\left|x\right|}{x+2}$-kx2=0 有1個不同的實數根
?$\frac{1}{x+2}$=k|x|有1個異根,
?函數y=$\frac{1}{x+2}$與y=k|x|有1個交點,
如圖示: ,
,
k>0時,由$\frac{1}{x+2}$=-kx得:kx2+2kx+1=0,
△=4k2-4k=0,解得:k=1,
結合圖象,k<0或0<k<1,
故答案為:k<0或0<k<1.
點評 本題主要考查函數零點和方程的根的關系,方程根的存在性以及個數判斷,二次函數的性質,體現了轉化、分類討論的數學思想,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{4}{21}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
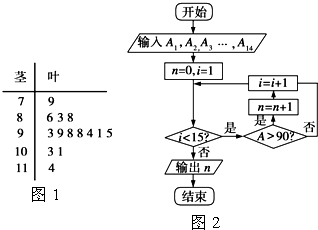 如圖1是某高三學生進入高中-二年來的數學考試成績莖葉圖,第1次到第 14次.考試成績依次記為A1,A2,…,A14.如圖2是統計莖葉圖中成績在一定范圍內考試次數的一個算法流程圖.那么算法流程圖輸出的結果是10.
如圖1是某高三學生進入高中-二年來的數學考試成績莖葉圖,第1次到第 14次.考試成績依次記為A1,A2,…,A14.如圖2是統計莖葉圖中成績在一定范圍內考試次數的一個算法流程圖.那么算法流程圖輸出的結果是10.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{3}{2}$,1) | B. | (-∞,1)∪($\frac{3}{2}$,+∞) | C. | (1,$\frac{3}{2}$) | D. | (-∞,1)∪[$\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=3cosx | B. | f(x)=x3+x2 | C. | f(x)=1+sin2x | D. | f(x)=ex+x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 正△ABC兩邊AB,AC的中點分別為M,N,直線MN與△ABC外接圓的一個交點為P.
正△ABC兩邊AB,AC的中點分別為M,N,直線MN與△ABC外接圓的一個交點為P.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com