
分析 求出函數的導數,得到切線的斜率,求出A的正切函數值,然后轉化利用正弦定理求解即可.
解答 解:函數y=lnx-$\frac{2}{x}$,可得y′=$\frac{1}{x}+\frac{2}{{x}^{2}}$,∴f′(1)=3,
∴tanA=3,可得sinA=$\sqrt{ta{n}^{2}A•co{s}^{2}A}=\sqrt{ta{n}^{2}A•\frac{1}{1+ta{n}^{2}a}}$=$\frac{3\sqrt{10}}{10}$,
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,可得sinB=$\frac{bsinA}{a}$=$\frac{3}{5}$.
故答案為:$\frac{3}{5}$.
點評 本題考查函數的導數的應用,三角函數的應用,正弦定理,考查計算能力.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:解答題
| 公園 | 甲 | 乙 | 丙 | 丁 |
| 獲得簽名人數 | 45 | 60 | 30 | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 1 | B. | $\sqrt{2015}$-1 | C. | $\sqrt{2016}$-1 | D. | $\sqrt{2017}$-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
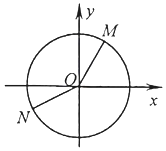
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
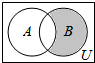
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com