
分析 先設p(x1,y1);Q(x2,y2),根據題設條件kop*koq=-1即;y1y2=-x1x2直線方程與雙曲線方程聯立,求得x1+x2=和x1x2的表達式,代入y1y2=-x1x2求得答案.
解答 解:設p(x1,y1),Q(x2,y2),
∵$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,
∴kop*koq=-1即;y1y2=-x1x2
聯立直線x+y-2=0和曲線$\frac{y^2}{b}$-$\frac{x^2}{a}$=1兩方程可得:(a-b)x2-4ax+4a-ab=0,
x1+x2=$\frac{4a}{a-b}$,x1x2=$\frac{4a-ab}{a-b}$,
y1y2=(2-x1)(2-x2)=4-2(x1+x2)+x1x2=-x1x2
即4-2•$\frac{4a}{a-b}$+$\frac{4a-ab}{a-b}$=-$\frac{4a-ab}{a-b}$,
即ab=2a-2b,
則$\frac{1}{b}$-$\frac{1}{a}$=$\frac{a-b}{ab}$=$\frac{1}{2}$.
故答案為:$\frac{1}{2}$.
點評 本題主要考查了雙曲線的應用.考查了學生綜合分析問題的能力,屬于中檔題.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 49 | B. | 45 | C. | 69 | D. | 73 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | m≤-$\frac{5}{4}$ | B. | m≤2 | C. | m≤$\frac{3}{4}$ | D. | m≤0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
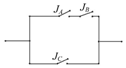 如圖,JA,JB兩個開關串聯再與開關JC并聯,在某段時間內每個開關能夠閉合的概率都是0.5,計算在這段時間內線路正常工作的概率為0.625.
如圖,JA,JB兩個開關串聯再與開關JC并聯,在某段時間內每個開關能夠閉合的概率都是0.5,計算在這段時間內線路正常工作的概率為0.625.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,+∞) | B. | (0,ln4) | C. | (ln4,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com