已知a，b，c為正數，用排序不等式證明：2（a3+b3+c3）≥a2（b+c）+b2（a+c）+c2（a+b）．
見解析
【解析】
試題分析：由（a3+b3）﹣（a2b+ab2）=（a+b）（a﹣b）2≥0，得a3+b3≥a2b+ab2，同理，a3+c3≥a2c+ac2，b3+c3≥b2c+bc2三式相加，能證明2（a3+b3+c3）≥a2（b+c）+b2（a+c）+c2（a+b）．
證明：先證明：a3+b3≥a2b+ab2，
∵（a3+b3）﹣（a2b+ab2）
=a2（a﹣b）﹣b2（a﹣b）
=（a2﹣b2）（a﹣b）
=（a+b）（a﹣b）2
≥0，
∴a3+b3≥a2b+ab2，取等號的條件是a=b，
同理，a3+b3≥a2b+ab2，
a3+c3≥a2c+ac2，
b3+c3≥b2c+bc2
三式相加，得：
2（a3+b3+c3）≥a2（b+c）+b2（a+c）+c2（a+b），
取等號的條件是a=b=c，
∴2（a3+b3+c3）≥a2（b+c）+b2（a+c）+c2（a+b）．
科目：高中數學 來源：[同步]2014年新人教A版選修4-6 1.2最大公因數與最小公倍數 題型：選擇題
在對16和12求最大公約數時，整個操作如下：（16，12）→（4，12）→（4，8）→（4，4），由此可以看出12和16的最大公約數是（ ）
A.4 B.12 C.16 D.8
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 4.2數學歸納法證明不等式舉例（解析版） 題型：填空題
用數學歸納法證明2n≥n2（n∈N，n≥1），則第一步應驗證 ．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 4.1數學歸納法練習卷（解析版） 題型：選擇題
用數學歸納法證明不等式“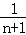
+
+…+
＞
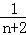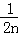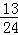（n＞2）”時的過程中，由n=k到n=k+1時，不等式的左邊（ ）
A.增加了一項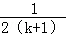
B.增加了兩項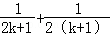
C.增加了兩項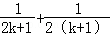，又減少了一項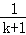
D.增加了一項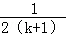，又減少了一項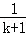
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 3.3排序不等式練習卷（解析版） 題型：解答題
設正整數構成的數列{an}使得a10k﹣9+a10k﹣8+…+a10k≤19對一切k∈N*恒成立．記該數列若干連續項的和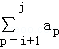
為S（i，j），其中i，j∈N*，且i＜j．求證：所有S（i，j）構成的集合等于N*．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 3.2一般形式柯西不等式練習卷（解析版） 題型：填空題
（2014•荊門模擬）已知實數a，b，c，d，e滿足a+b+c+d+e=8，a2+b2+c2+d2+e2=16，則e的取值范圍是 ．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 3.2一般形式柯西不等式練習卷（解析版） 題型：選擇題
已知a，b，c∈R，且a+b+c=0，abc＞0，則
+
+
的值（ ）
A.小于0 B.大于0 C.可能是0 D.正負不能確定
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 3.1二維形式柯西不等式練習卷（解析版） 題型：選擇題
已知a，b∈R，a2+b2=4，求3a+2b的取值范圍為（ ）
A.3a+2b≤4 B.3a+2b≤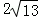
C.3a+2b≥4 D.不確定
查看答案和解析>>
科目：高中數學 來源：[同步]2014年新人教A版選修4-5 2.1比較法練習卷（解析版） 題型：填空題
設a，b，c∈（﹣∞，0），則對于a+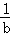
，b+
，c+
，下列正確的是
①都不大于﹣2
②都不小于﹣2
③至少有一個不小于﹣2
④至少有一個不大于﹣2．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com